
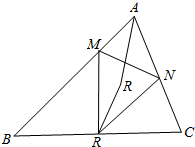
 已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上.
已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上. 分析 由已知得点M、N分别在线段AB、AC内,在射线AR上取一点R1,使A、M、R1、N四点共圆,由AB≠AC,得到∠MON的平分线与∠BAC的平分线有惟一交点R,从而得到R1=R,即A、M、R、N四点共圆.设AR的延长线交BC于点K,则K在边BC上,由已知条件推导出B、M、R、K四点共圆,C、N、R、K四点共圆.由此能证明△BMR的外接圆和△CNR的外接圆有一个交点在BC上.
解答 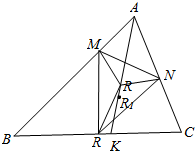 证明:如图,先证明A、M、R、N四点共圆,
证明:如图,先证明A、M、R、N四点共圆,
∵△ABC为锐角三角形,∴点M、N分别在线段AB、AC内,
在射线AR上取一点R1,使A、M、R1、N四点共圆,
∵AR1平分∠BAC,∴R1M=R1N,
∵OM=ON,R1M=R1N,∴R1在∠MON的平分线上,
∵AB≠AC,∴∠MON的平分线与∠BAC的平分线不重合、不平行,有惟一交点R,
∴R1=R,即A、M、R、N四点共圆.
其次,设AR的延长线交BC于点K,则K在边BC上,
∵B、C、N、M四点共圆,∴∠MBC=∠ANM,
∵A、M、R、N四点共圆,∴∠MBK=∠MRA,
∴B、M、R、K四点共圆,
同理,C、N、R、K四点共圆.
故△BMR的外接圆和△CNR的外接圆有一个交点在BC上.
点评 本题考查四点共圆的证明与应用,是中档题,解题时要认真审题,注意四点共圆的性质的合理运用.


科目:高中数学 来源: 题型:解答题
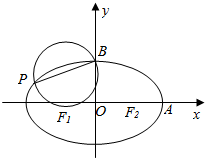 设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.
设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
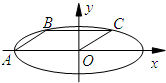 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
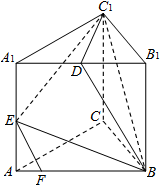 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
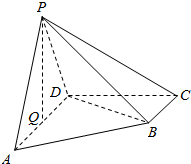 四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.
四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | ||
| C. | A∩B=∅ | D. | 集合A、B间没有包含关系 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com