
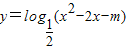 的值域为R;
的值域为R; 在定义域上是奇函数”的充分不必要条件;
在定义域上是奇函数”的充分不必要条件;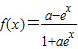 在定义域上是奇函数时,a=1,可得④不正确.
在定义域上是奇函数时,a=1,可得④不正确.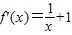 ,∴函数在区间(1,e)上单调递增,f(1)=-1,f(e)=e-1>0,根据函数零点的判定定理可得,在区间(1,e)上存在零点,故①正确.
,∴函数在区间(1,e)上单调递增,f(1)=-1,f(e)=e-1>0,根据函数零点的判定定理可得,在区间(1,e)上存在零点,故①正确.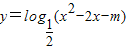 的真数为x2-2x-m,判别式△=4+4m≥0,故真数可取遍所有的正实数,所以函数
的真数为x2-2x-m,判别式△=4+4m≥0,故真数可取遍所有的正实数,所以函数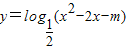 的值域为R,故③正确.
的值域为R,故③正确.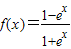 f(x)=定义域为R,关于原点对称
f(x)=定义域为R,关于原点对称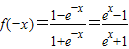 =-f(x),故函数在定义域上是奇函数,故充分性成立.
=-f(x),故函数在定义域上是奇函数,故充分性成立.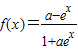 在定义域上是奇函数,则有f(0)=0,∴a=1,故必要性成立,故“a=1”是“函数
在定义域上是奇函数,则有f(0)=0,∴a=1,故必要性成立,故“a=1”是“函数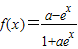 在定义域上是奇函数”的充分必要条件,故④不正确.
在定义域上是奇函数”的充分必要条件,故④不正确.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| a-ex |
| 1+aex |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
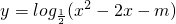 的值域为R;
的值域为R;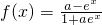 在定义域上是奇函数”的充分不必要条件;
在定义域上是奇函数”的充分不必要条件;查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省菏泽市郓城一中高三(上)11月月考数学试卷(理科)(解析版) 题型:填空题
 的值域为R;
的值域为R;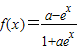 在定义域上是奇函数”的充分不必要条件;
在定义域上是奇函数”的充分不必要条件;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com