
三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1中点.
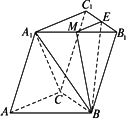
(1)求证:BM⊥AC.
(2)求二面角B-B1C1-A1的正切值.
(3)求三棱锥M-A1CB的体积.
|
解:(1)∵ABB1A1是菱形,∠A1AB=60°,则△A1B1B是正三角形. 又∵M是A1B1中点, ∴BM⊥A1B1. 又∵平面AA1B1B⊥平面A1B1C, ∴BM⊥平面A1B1C1, ∴BM⊥A1C1, 又∵AC∥A1C1, ∴BM⊥AC. (2)过M作ME⊥B1C1且交于点E, ∵BM⊥平面A1B1C1, ∴BE⊥B1C1, ∴∠BEM为所求二面角的平面角. 在△A1B1C1中,ME=MB1sin60°= Rt△BMB1中,MB=BB1sin60°= ∴tan∠BEM= (3)VM-A1CB= = |
|
本题考查空间的垂直关系,空间角及几何体的计算问题.注意运用三垂线定理作证二面角的平面角,以及等积变换法求几何体的体积. |


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
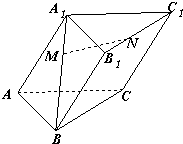 三棱柱ABC-A1B1C1中,M、N分别是A1B、B1C1上的点,且BM=2A1M,C1N=2B1N.设
三棱柱ABC-A1B1C1中,M、N分别是A1B、B1C1上的点,且BM=2A1M,C1N=2B1N.设| AB |
| a |
| AC |
| b |
| AA1 |
| c |
| a |
| b |
| c |
| MN |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A1B1C1D1中,点M是A1B的中点,点N是B1C的中点,连接MN.
如图,在直三棱柱ABC-A1B1C1D1中,点M是A1B的中点,点N是B1C的中点,连接MN.| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
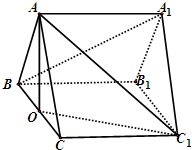 (2011•浙江模拟)已知三棱柱ABC-A1B1C1,底面△ABC为正三角形,AA1⊥平面ABC,BC=
(2011•浙江模拟)已知三棱柱ABC-A1B1C1,底面△ABC为正三角形,AA1⊥平面ABC,BC=| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com