已知函数f(x)=x3+ax2+bx+a2(a、b∈R).
(1)当a=0,b=-3时,求函数f(x)在[-1,3]上的最大值;
(2)若函数f(x)在x=1处有极值10,求f(x)的解析式;
(3)当a=-2时,若函数f(x)在[2,+∞)上是单调增函数,求b的取值范围.
【答案】
分析:(1)把a=0,b=-3代入原函数,求出原函数的导函数,由导函数的零点对定义域分段,通过列表分析导函数在各区间段内的符号,得到原函数在各区间段内的单调性,找出极值点,求出极值,求出闭区间的端点处的函数值,则函数f(x)在[-1,3]上的最大值可求;
(2)由函数f(x)在x=1处有极值10,则f
′(1)=0,f(1)=10,联立后可求a,b的值,则函数解析式可求;
(3)把a=-2代入原函数解析式,然后求其导函数,由函数f(x)在[2,+∞)上是单调增函数,得到f'(2)≥0,由此可求b的取值范围.
解答:解:(1)当a=0,b=-3时,f(x)=x
3-3x,
所以f′(x)=3x
2-3,
令 f′(x)=0,解得 x
1=-1,x
2=1
列表:
| x | -1 | (-1,1) | 1 | (1,3) | 3 |
| f′(x) | | - | | + | |
| f(x) | 极大值2 | 减函数 | 极小值-2 | 增函数 | 18 |
从上表可知,函数f(x)在[-1,3]上的最大值为18.
(2)因为f(x)=x
3+ax
2+bx+a
2,所以f'(x)=3x
2+2ax+b,
由已知条件,得
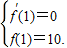
即
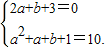
解得
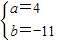
或
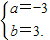
下面分别检验:
①当a=4,b=-11时,f(x)=x
3+4x
2-11x+16,f′(x)=3x
2+8x-11,
令f′(x)=0,即 3x
2+8x-11=0,解得
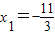
,x
2=1,
列表:
| x | 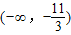 | 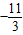 |  | 1 | (1,+∞) |
| f′(x) | + | | - | | + |
| f(x) | 增函数 | 极大值 | 减函数 | 极小值10 | 增函数 |
由上表可知,f(x)在x=1处取极小值10,符合题意.
②当a=-3,b=3时,f(x)=x
3-3x
2+3x+9,f′(x)=3x
2-6x+3=3(x
2-2x+1)=3(x-1)
2≥0,f(x)为增函数,不合题意,舍去.
所以当a=4,b=-11时,f(x)=x
3+4x
2-11x+16为所求函数的解析式.
综上所述,所求函数的解析式为f(x)=x
3+4x
2-11x+16.
(3)当a=-2时,f(x)=x
3-2x
2+bx+4,f'(x)=3x
2-4x+b,
此导函数是二次函数,二次项系数大于0,且对称轴为
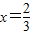
,
因为函数f(x)在[2,+∞)上单调递增,所以f
′(x)≥0在[2,+∞)上恒成立,
也就是f'(2)≥0,
即 3×2
2-4×2+b≥0,解得b≥-4,
所以,b的取值范围是[-4,+∞).
点评:本题考查了利用导数研究函数的单调性,函数在某区间上是单调函数,则函数的导函数在该区间上恒大于等于0或恒小于等于0,考查了函数解析式得求解及常用方法,利用了函数在极值点处的导数等于0,考查了利用导数研究函数的最值,此题属中档题.

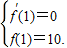 即
即 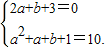
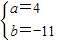 或
或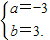
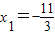 ,x2=1,
,x2=1,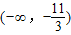
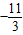

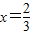 ,
,

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<