
【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
R(x)=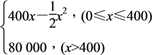
其中x是仪器的月产量.
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少元?(总收益=总成本+利润)
【答案】(1)f(x)=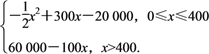 ;(2)每月生产300台仪器时,利润最大,最大利润为25 000元.
;(2)每月生产300台仪器时,利润最大,最大利润为25 000元.
【解析】试题分析:(1)利润=收益-成本,由已知分两段当![]() 时,和当
时,和当![]() 时,即可求出利润函数的解析式;(2)分别求出两段函数的最大值,两者大者为所求利润最大值.
时,即可求出利润函数的解析式;(2)分别求出两段函数的最大值,两者大者为所求利润最大值.
试题解析: (1)设月产量为x台,则总成本为20 000+100x,从而
f(x)=
(2)当0≤x≤400时,
f(x)=-![]() (x-300)2+25 000.
(x-300)2+25 000.
∴当x=300时,f(x)的最大值为25 000;
当x>400时,
f(x)=60 000-100x是减函数,
f(x)<60 000-100×400=20 000<25 000.
∴当x=300时,f(x)的最大值为25 000,
即每月生产300台仪器时,利润最大,最大利润为25 000元.


科目:高中数学 来源: 题型:
【题目】【2014陕西理8】原命题为“若![]() 互为共轭复数,则
互为共轭复数,则![]() ”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
A. 真,假,真 B. 假,假,真
C. 真,真,假 D. 假,假,假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A对应________;B对应________;C对应________;D对应________.
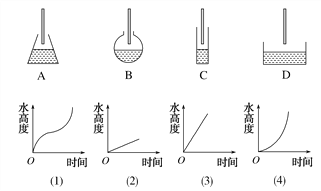
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每个月可卖出
元,每个月可卖出![]() 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨![]() 元,则每个月少卖
元,则每个月少卖![]() 件(每件售价不能高于
件(每件售价不能高于![]() 元).设每件商品的售价上涨
元).设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
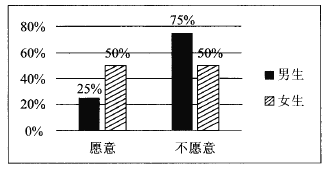
(1)根据条件完成下列![]() 列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者,再从中抽取2人参加挑战,求抽取的2人中至少有一名男生的概率.
参考数据及公式:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
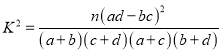 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
销售收入y | 16 | 23 | 25 | 26 | 30 |
(1)求y关于x的回归方程; (2)2017年度该电商准备投入广告费1.5亿元,
利用(1)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 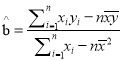
![]() ,选用数据:
,选用数据: ![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com