
【题目】已知函数
f(x)=(cosx﹣x)(π+2x)﹣ ![]() (sinx+1)
(sinx+1)
g(x)=3(x﹣π)cosx﹣4(1+sinx)ln(3﹣ ![]() )
)
证明:
(1)存在唯一x0∈(0, ![]() ),使f(x0)=0;
),使f(x0)=0;
(2)存在唯一x1∈( ![]() ,π),使g(x1)=0,且对(Ⅰ)中的x0 , 有x0+x1<π.
,π),使g(x1)=0,且对(Ⅰ)中的x0 , 有x0+x1<π.
【答案】
(1)证明:∵当x∈(0, ![]() )时,f′(x)=﹣(1+sinx)(π+2x)﹣2x﹣
)时,f′(x)=﹣(1+sinx)(π+2x)﹣2x﹣ ![]() cosx<0,
cosx<0,
∴函数f(x)在(0, ![]() )上为减函数,
)上为减函数,
又f(0)=π﹣ ![]() >0,f(
>0,f( ![]() )=﹣π2﹣
)=﹣π2﹣ ![]() <0;
<0;
∴存在唯一的x0∈(0, ![]() ),使f(x0)=0;
),使f(x0)=0;
(2)证明:考虑函数h(x)= ![]() ﹣4ln(3﹣
﹣4ln(3﹣ ![]() x),x∈[
x),x∈[ ![]() ,π],
,π],
令t=π﹣x,则x∈[ ![]() ,π]时,t∈[0,
,π]时,t∈[0, ![]() ],
],
记函数u(t)=h(π﹣t)= ![]() ﹣4ln(1+
﹣4ln(1+ ![]() t),
t),
则u′(t)= ![]() ﹣
﹣ ![]()
![]()
= ![]() ﹣
﹣ ![]()
= ![]() ﹣
﹣ ![]()
= ![]()
= ![]() ,
,
由(Ⅰ)得,当t∈(0,x0)时,u′(t)>0;
在(0,x0)上u(x)是增函数,又u(0)=0,∴当t∈(0,x0]时,u(t)>0,
∴u(t)在(0,x0]上无零点;
在(x0, ![]() )上u(t)是减函数,且u(x0)>0,u(
)上u(t)是减函数,且u(x0)>0,u( ![]() )=﹣4ln2<0,
)=﹣4ln2<0,
∴存在唯一的t1∈(x0, ![]() ),使u(t1)=0;
),使u(t1)=0;
∴存在唯一的t1∈(0, ![]() ),使u(t1)=0;
),使u(t1)=0;
∴存在唯一的x1=π﹣t1∈( ![]() ,π),使h(x1)=h(π﹣t1)=u(t1)=0;
,π),使h(x1)=h(π﹣t1)=u(t1)=0;
∵当x∈( ![]() ,π)时,1+sinx>0,∴g(x)=(1+sinx)h(x)与h(x)有相同的零点,
,π)时,1+sinx>0,∴g(x)=(1+sinx)h(x)与h(x)有相同的零点,
∴存在唯一的x1∈( ![]() ,π),使g(x1)=0,
,π),使g(x1)=0,
∵x1=π﹣t1,t1>x0,∴x0+x1<π.
【解析】(1)根据x∈(0, ![]() )时,f′(x)<0,得出f(x)是单调减函数,
)时,f′(x)<0,得出f(x)是单调减函数,
再根据f(0)>0,f( ![]() )<0,得出此结论;(2)构造函数h(x)=
)<0,得出此结论;(2)构造函数h(x)= ![]() ﹣4ln(3﹣
﹣4ln(3﹣ ![]() x),x∈[
x),x∈[ ![]() ,π],令t=π﹣x,得u(t)=h(π﹣t),求出u(t)存在唯一零点t1∈(0,
,π],令t=π﹣x,得u(t)=h(π﹣t),求出u(t)存在唯一零点t1∈(0, ![]() ),即证g(x)存在唯一的零点x1∈(
),即证g(x)存在唯一的零点x1∈( ![]() ,π),满足x0+x1<π.
,π),满足x0+x1<π.
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个数字中任取
这五个数字中任取![]() 个组成无重复数字的三位数,当三个数字中有
个组成无重复数字的三位数,当三个数字中有![]() 和
和![]() 时,
时,![]() 需排在
需排在![]() 的前面(不一定相邻),这样的三位数有( )个.
的前面(不一定相邻),这样的三位数有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的广告支出x(单位:万元)与销售收入y(单位:万元)之间有下表所对应的数据:
广告支出x(单位:万元) | 1 | 2 | 3 | 4 |
销售收入y(单位:万元) | 12 | 28 | 42 | 56 |
(1)画出表中数据的散点图;
(2)求出y对x的回归直线方程![]() ;
;
(3)若广告费为9万元,则销售收入约为多少万元?
参考公式: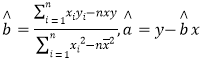
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月9-25日,第23届冬奥会在韩国平昌举行.4年后,第24 届冬奥会将在中国北京和张家口举行.为了宣传冬奥会,某大学在平昌冬奥会开幕后的第二天,从全校学生中随机抽取了120名学生,对是否收看平昌冬奥会开幕式情况进行了问卷调查,统计数据如下:

(1)根据上表说明,能否有![]() 的把握认为,收看开幕式与性别有关?
的把握认为,收看开幕式与性别有关?
(2)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法,选取12人参加2022年北京冬奥会志愿者宣传活动.若从这12人中随机选取3人到校广播站开展冬奥会及冰雪项目的宣传介绍,设选取的3 人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了![]() 件产品作为样本逐件称出它们的重量(单位:克),重量值落在
件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求出甲(同组中的重量值用组中点值代替)方案样本中![]() 件产品的平均数;
件产品的平均数;
(2)若以频率作为概率,试估计从两种方案分别任取![]() 件产品,恰好两件产品都是合格品的概率分别是多少;
件产品,恰好两件产品都是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式: 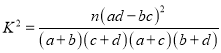 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2|x﹣1|+x﹣1,g(x)=16x2﹣8x+1.记f(x)≤1的解集为M,g(x)≤4的解集为N.
(1)求M;
(2)当x∈M∩N时,证明:x2f(x)+x[f(x)]2≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+bx+b) ![]() (b∈R)
(b∈R)
(1)当b=4时,求f(x)的极值;
(2)若f(x)在区间(0, ![]() )上单调递增,求b的取值范围.
)上单调递增,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班![]() 名同学的数学小测成绩的频率分布表如图所示,其中
名同学的数学小测成绩的频率分布表如图所示,其中![]() ,且分数在
,且分数在![]() 的有
的有![]() 人.
人.
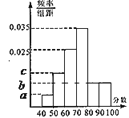
(1)求![]() 的值;
的值;
(2)若分数在![]() 的人数是分数在
的人数是分数在![]() 的人数的
的人数的![]() ,求从不及格的人中任意选取3人,其中分数在50分以下的人数为
,求从不及格的人中任意选取3人,其中分数在50分以下的人数为![]() ,求
,求![]() 的数学期.
的数学期.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com