
|
| 2 |
| π |
| 4 |
| 2 |
|
| 2 |
| π |
| 4 |
|
| 2 |
| 2 | ||
|
| 2 |
| 5 |
| 5 |
| 2 |


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 4 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三第四次高考仿真测试文科数学试卷(解析版) 题型:解答题
选修4-4:极坐标与参数方程:
已知椭圆C的极坐标方程为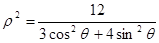 ,点
,点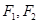 为其左,右焦点,直线
为其左,右焦点,直线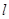 的参数方程为
的参数方程为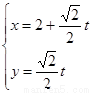 (
(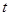 为参数,
为参数,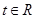 ).
).
(Ⅰ)求直线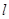 和曲线C的普通方程;
和曲线C的普通方程;
(Ⅱ)求点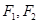 到直线
到直线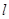 的距离之和.
的距离之和.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省扬州市宝应县高三下学期期初测试数学试卷 题型:解答题
(本题满分10分,选修4-4:极坐标与参数方程)
已知圆C的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (t是参数)。
(t是参数)。
若直线 与圆C相切,求实数m的值.
与圆C相切,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com