
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据相关系数r的性质进行判断,
②根据期望和方差的定义和性质进行判断,
③根据正态分布的性质进行求解.
④比较当n=k和n=k+1时,左边项的变化进行判断.
解答 解:①两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值越接近于0,表示两个变量之间几乎不存在线性相关,故①不正确;
②将一组数据中的每个数据都加上同一个非零常数后,期望改变,方差不变,正确,故②正确,
③某厂生产的零件外直径x~N(3,1),且p(2≤x≤4)=0.68,则p(3≤x≤4)=0.34,则p(x<4)=0.34+0.5=0.84,故③正确,
④用数学归纳法证明不等式$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<$\frac{13}{14}$(n≥2,n∈{N*)的过程中,
当n=k时,左边为$\frac{1}{k+1}$+$\frac{1}{k+2}$+…+$\frac{1}{2k}$,
当n=k+1时,左边为$\frac{1}{k+2}$+…+$\frac{1}{2k}$+$\frac{1}{2k+1}$+$\frac{1}{2k+2}$=$\frac{1}{k+1}$+$\frac{1}{k+2}$+…+$\frac{1}{2k}$+($\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k+1}$),
故左边增加的项是$\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k+1}$,故④错误,
故正确的是②③,
故选:B
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,但难度不大.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 2 | C. | -4或-$\frac{1}{4}$ | D. | -2或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | $(-1+\sqrt{3},1)∪(-3,-1-\sqrt{3})$ | C. | $(-1-\sqrt{3},-1+\sqrt{3})$ | D. | $(-∞,-1-\sqrt{3})∪(-1+\sqrt{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 定义域是[-1,1] | B. | f(x)是奇函数 | ||
| C. | 值域是[-tan1,tan1] | D. | 在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
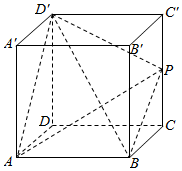 在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.
在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在多面体SP-ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.
已知在多面体SP-ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{3}$) | B. | (-∞,0] | C. | (-∞,1) | D. | (-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com