
【题目】函数![]() .
.
(1)当![]() ,
, ![]() 时,求
时,求![]() 的单调减区间;
的单调减区间;
(2)![]() 时,函数
时,函数![]() ,若存在
,若存在![]() ,使得
,使得![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料3千克;生产乙产品1桶需耗
原料3千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克,每桶甲产品的利润是300元,每桶乙产品的利润是400元,公司在要求每天消耗
原料1千克,每桶甲产品的利润是300元,每桶乙产品的利润是400元,公司在要求每天消耗![]() 原料都不超过12千克的条件下,生产产品
原料都不超过12千克的条件下,生产产品![]() 、产品
、产品![]() 的利润之和的最大值为( )
的利润之和的最大值为( )
A. 1800元 B. 2100元 C. 2400元 D. 2700元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(1﹣x)+loga(x+3),(0<a<1).
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣2,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点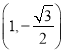 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如表的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 ![]()
(1)请完成如表的列联表;
(2)根据列联表的数据,有多大的把握认为“成绩与班级有关系“?
(3)按分层抽样的方法,从优秀学生中抽出6名学生组成一个样本,再从样本中抽出2名学生,记甲班被抽到的人数为ξ,求ξ的分布列和数学期望.
参考公式和数据:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
下面的临界值表供参考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,﹣4),且倾斜角为 ![]() ,圆C的极坐标方程为ρ=4cosθ.
,圆C的极坐标方程为ρ=4cosθ.
(1)求直线l的参数方程和圆C的直角坐标方程;
(2)若直线l和圆C相交于A、B两点,求|PA||PB|及弦长|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出![]() 次成功交易,并对其评价进行统计爱,商品和服务评价的
次成功交易,并对其评价进行统计爱,商品和服务评价的![]() 列联表如下表:
列联表如下表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 |
|
|
|
对商品不满意 |
|
|
|
合计 |
|
|
|
(1)是否可以在犯错误概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的![]() 次购物中,设对商品和服务全好评的次数为随机变量
次购物中,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(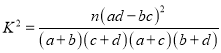 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com