
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)判断并证明![]() )在
)在![]() )上的单调性;
)上的单调性;
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 为奇函数;(2)证明见解析;(3)
为奇函数;(2)证明见解析;(3)![]() .
.
【解析】试题分析:
本题考查函数奇偶性的判断和单调性的证明,以及根据恒成立问题求参数取值范围。(1)根据奇偶性的判断方法证明。(2)根据单调性的判断方法证明。(3)根据函数的单调性将函数不等式转化为一般不等式,通过分离参数的方法转化为求具体函数的最值问题处理。
试题解析:
(1)![]() 定义域R关于原点对称,
定义域R关于原点对称,
∵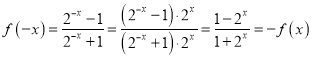 ,
,
![]() 为奇函数.
为奇函数.
(2)证明:设![]() R,且
R,且![]() ,
,
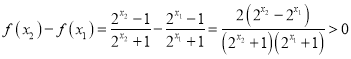 ,
,
∵函数 ![]() 在
在 ![]() 上为增函数,
上为增函数,
![]() ,故
,故![]() ,
,
![]() .
.
∴函数![]() 在
在![]() 上是增函数 .
上是增函数 .
(3)![]()
![]() ,
,
又![]() 为奇函数,
为奇函数,
![]() ,
,
∵![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 上为增函数,
上为增函数,
∴当![]() 时,函数
时,函数![]() 取得最小值,且
取得最小值,且![]() 。
。
∴![]() 。
。
故实数![]() 的取值范围为
的取值范围为![]() 。
。


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的倾斜角为
的倾斜角为 ![]() 且经过点
且经过点 ![]() .
.
(1)以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线 ![]() 的极坐标方程;
的极坐标方程;
(2)设直线 ![]() 与曲线
与曲线 ![]() 交于两点
交于两点 ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为 ![]() 的等比数列
的等比数列 ![]() 是递减数列,且
是递减数列,且 ![]() ,
, ![]() ,
, ![]() 成等差数列;数列
成等差数列;数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,且
,且 ![]() ,
, ![]()
(Ⅰ)求数列 ![]() ,
, ![]() 的通项公式;
的通项公式;
(Ⅱ)已知 ![]() ,求数列
,求数列 ![]() 的前
的前 ![]() 项和
项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为R
的定义域为R
(1)当a=2时,求函数f(x)的值域
(2)若函数f(x)是奇函数,①求a的值;②解不等式f(3﹣m)+f(3﹣m2)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com