
【题目】已知函数![]() (
(![]() ,e为自然对数的底数).
,e为自然对数的底数).
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)若![]() 在R上单调递减,
在R上单调递减,
①求a的取值范围;
②当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)1;(2)①![]() ,②证明见解析.
,②证明见解析.
【解析】
(1)求出函数的导函数,利用导函数与函数单调性的关系当![]() ,求出单调递增区间,当
,求出单调递增区间,当![]() ,求出函数的单调递减区间,进而可求出最大值.
,求出函数的单调递减区间,进而可求出最大值.
(2)①求出![]() 对
对![]() 恒成立,化为
恒成立,化为![]() 对
对![]() 恒成立,记
恒成立,记![]() ,讨论
,讨论![]() 值,求出
值,求出![]() 的最小值即可证出;②由题意可得
的最小值即可证出;②由题意可得![]() ,即
,即![]() ,两边取对数可得
,两边取对数可得![]() ,下面采用分析法即可证出.
,下面采用分析法即可证出.
(1)![]() 时,
时,![]()
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增
上单调递增
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
![]()
(2)由![]()
①![]() 在R上单调递减,
在R上单调递减,![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,记
恒成立,记![]() ,
,
则![]() 对
对![]() 恒成立,
恒成立,![]()
当![]() 时,
时,![]() ,符题
,符题
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;![]()
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
![]()
综上:![]()
②当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
要证![]() ,即证
,即证![]()
下面证明![]()
令![]() ,
,![]() ,则
,则![]() ,
,
![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() ,得证
,得证![]()


科目:高中数学 来源: 题型:
【题目】某日A, B, C三个城市18个销售点的小麦价格如下表:
销售点序号 | 所属城市 | 小麦价格(元/吨) | 销售点序号 | 所属城市 | 小麦价格(元/吨) |
1 | A | 2420 | 10 | B | 2500 |
2 | C | 2580 | 11 | A | 2460 |
3 | C | 2470 | 12 | A | 2460 |
4 | C | 2540 | 13 | A | 2500 |
5 | A | 2430 | 14 | B | 2500 |
6 | C | 2400 | 15 | B | 2450 |
7 | A | 2440 | 16 | B | 2460 |
8 | B | 2500 | 17 | A | 2460 |
9 | A | 2440 | 18 | A | 2540 |
(Ⅰ)求B市5个销售点小麦价格的中位数;
(Ⅱ)甲从B市的销售点中随机挑选一个购买1吨小麦,乙从C市的销售点中随机挑选一个购买1吨小麦,求甲花费的费用比乙高的概率;
(Ⅲ)如果一个城市的销售点小麦价格方差越大,则称其价格差异性越大.请你对A、B、C三个城市按照小麦价格差异性从大到小进行排序(只写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
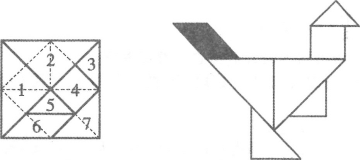
【题目】七巧板是一种古老的中国传统智力玩具,是由七块板组成的.而这七块板可拼成许多图形,例如:三角形、不规则多边形、各种人物、动物、建筑物等,清陆以湉《冷庐杂识》写道:近又有七巧图,其式五,其数七,其变化之式多至千余.在18世纪,七巧板流传到了国外,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.若用七巧板拼成一只雄鸡,在雄鸡平面图形上随机取一点,则恰好取自雄鸡鸡尾(阴影部分)的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校为增加应届毕业生就业机会,每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估,已知某年度参与评估的毕业生共有2000名,其评估成绩![]() 近似的服从正态分布
近似的服从正态分布![]() .现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
.现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
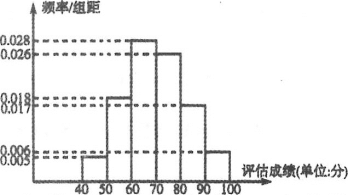
(1)求样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若学校规定评估成绩超过![]() 分的毕业生可参加
分的毕业生可参加![]() 三家公司的面试.
三家公司的面试.
(ⅰ)用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
(ⅱ)若三家公司每家都提供甲、乙、丙三个岗位,岗位工资表如下:
公司 | 甲岗位 | 乙岗位 | 丙岗位 |
| 9600 | 6400 | 5200 |
| 9800 | 7200 | 5400 |
| 10000 | 6000 | 5000 |
李华同学取得了三个公司的面试机会,经过评估,李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为![]() ,李华准备依次从
,李华准备依次从![]() 三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择
三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择![]() 公司的哪些岗位?
公司的哪些岗位?
并说明理由.
附:![]() ,若随机变量
,若随机变量![]() ,
,
则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() ,平面
,平面![]() 平面ABE,四边形ABCD为矩形,
平面ABE,四边形ABCD为矩形,![]() ,F为CE上的点,且
,F为CE上的点,且![]() 平面ACE.
平面ACE.

(1)求证:![]() ;
;
(2)设M在线段DE上,且满足![]() ,试在线段AB上确定一点N,使得
,试在线段AB上确定一点N,使得![]() 平面BCE,并求MN的长.
平面BCE,并求MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题的个数是( )
①若“p∨q”为真命题,则“p∧q”为真命题;
②“a∈(0,+∞),函数y=![]() 在定义域内单调递增”的否定;
在定义域内单调递增”的否定;
③l为直线,α,β为两个不同的平面,若l⊥β,α⊥β,则l∥α;
④“x∈R,![]() ≥0”的否定为“
≥0”的否定为“![]() R,
R,![]() <0”.
<0”.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是新兵训练时,某炮兵连![]() 周中炮弹对同一目标的命中的情况的柱状图:
周中炮弹对同一目标的命中的情况的柱状图:
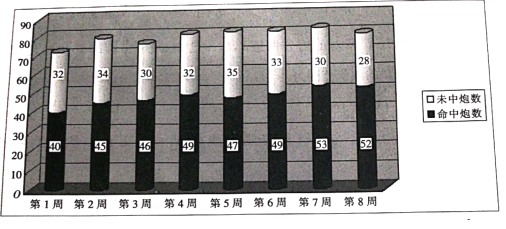
(1)计算该炮兵连这![]() 周中总的命中频率
周中总的命中频率![]() ,并确定第几周的命中频率最高;
,并确定第几周的命中频率最高;
(2)以(1)中的![]() 作为该炮兵连甲对同一目标的命中率,若每次发射相互独立,且炮兵甲发射
作为该炮兵连甲对同一目标的命中率,若每次发射相互独立,且炮兵甲发射![]() 次,记命中的次数为
次,记命中的次数为![]() ,求
,求![]() 的方差;
的方差;
(3)以(1)中的![]() 作为该炮兵连炮兵对同一目标的命中率,试问至少要用多少枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过
作为该炮兵连炮兵对同一目标的命中率,试问至少要用多少枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过![]() (取
(取![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com