
【题目】已知定义在![]() 上的函数
上的函数![]() ,
,![]() 为其导数,且
为其导数,且![]() 恒成立,则( )
恒成立,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
通过![]() ,可以联想到导数运算的除法,这样可以构造新函数
,可以联想到导数运算的除法,这样可以构造新函数
![]() ,
,![]() ,这样就可以判断出函数
,这样就可以判断出函数![]() 在
在![]() 上的单调性,把四个选项变形,利用单调性判断出是否正确.
上的单调性,把四个选项变形,利用单调性判断出是否正确.
通过![]() ,这个结构形式,可以构造新函数
,这个结构形式,可以构造新函数![]() ,
,
![]() ,而
,而![]() ,所以当
,所以当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上是单调递增函数,现对四个选项逐一判断:
上是单调递增函数,现对四个选项逐一判断:
选项A. ![]() ,可以判断
,可以判断![]() 是否正确,
是否正确,
也就是判断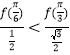 是否正确,即判断
是否正确,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,故选项A正确;
,故选项A正确;
选项B.![]() ,也就是判断
,也就是判断![]() 是否正确,即判断
是否正确,即判断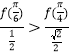 是否成立,即判断
是否成立,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,故选项B不正确;
,故选项B不正确;
选项C. ![]() ,也就是判断
,也就是判断![]() 是否正确,即判断
是否正确,即判断
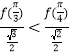 是否成立,即判断
是否成立,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,故选项C不正确;
,故选项C不正确;
选项D.![]() ,也就是判断
,也就是判断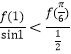 ,是否成立,即判断
,是否成立,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,因此选项D不正确,故本题选A.
,因此选项D不正确,故本题选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() 为实常数.
为实常数.
(1)若函数![]() 在区间[2,3]上为单调递增函数,求
在区间[2,3]上为单调递增函数,求![]() 的取值范围;
的取值范围;
(2)高函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,试讨论函数
,试讨论函数![]() ,
,![]() 的零点的情况.
的零点的情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥![]() ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱![]() (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高![]() 是正四棱锥的高
是正四棱锥的高![]() 的4倍.
的4倍.

(1)若![]() 则仓库的容积是多少?
则仓库的容积是多少?
(2)若正四棱锥的侧棱长为![]() ,则当
,则当![]() 为多少时,仓库的容积最大?
为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为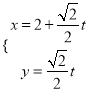 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地植被面积 ![]() (公顷)与当地气温下降的度数
(公顷)与当地气温下降的度数![]() (
(![]() )之间有如下的对应数据:
)之间有如下的对应数据:
| 20 | 40 | 50 | 60 | 80 |
| 3 | 4 | 4 | 4 | 5 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少![]() ?
?
参考公式:用最小二乘法求线性回归方程系数公式: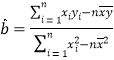 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过圆![]() 与
与![]() 轴正半轴的交点A作圆O的切线
轴正半轴的交点A作圆O的切线![]() ,M为
,M为![]() 上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线
上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线![]() 上运动时,△MAQ的垂心的轨迹方程为________.
上运动时,△MAQ的垂心的轨迹方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l:![]() -y+3+
-y+3+![]() =0和圆
=0和圆![]() :
:![]() +
+![]() +8x+F=0.若直线l被圆
+8x+F=0.若直线l被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 和x轴相交于A,B两点,点P为圆
和x轴相交于A,B两点,点P为圆![]() 上不同于A,B的任意一点,直线PA,PB交y轴于M,N两点.当点P变化时,以MN为直径的圆
上不同于A,B的任意一点,直线PA,PB交y轴于M,N两点.当点P变化时,以MN为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论;
内一定点?请证明你的结论;
(3)若△RST的顶点R在直线x=-1上,点S,T在圆![]() 上,且直线RS过圆心
上,且直线RS过圆心![]() ,∠SRT=
,∠SRT=![]() ,求点R的纵坐标的范围.
,求点R的纵坐标的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com