
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有两个元素,求
的解集中恰有两个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)当a=1时,利用对数函数的单调性,直接解不等式f(x)![]() 1即可;
1即可;
(2)化简关于x的方程f(x)+2x=0,通过分离变量推出a的表达式,通过解集中恰有两个元素,利用二次函数的性质,即可求a的取值范围;
(3)在R上单调递减利用复合函数的单调性,求解函数的最值,∴令![]() ,化简不等式,转化为求解不等式的最大值,然后求得a的范围.
,化简不等式,转化为求解不等式的最大值,然后求得a的范围.
(1)当![]() 时,
时,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴原不等式的解集为![]() .
.
(2)方程![]() ,
,
即为![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,则
,则![]() ,
,
由题意得方程![]() 在
在![]() 上只有两解,
上只有两解,
令![]() ,
, ![]() ,
,
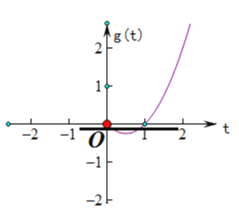
结合图象可得,当![]() 时,直线
时,直线![]() 和函数
和函数![]() 的图象只有两个公共点,
的图象只有两个公共点,
即方程只有两个解.
∴实数![]() 的范围
的范围![]() .
.
(3)∵函数![]() 在
在![]() 上单调递减,
上单调递减,
∴函数![]() 在定义域内单调递减,
在定义域内单调递减,
∴函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
最小值为![]() ,
,
∴![]() ,
,
由题意得![]() ,
,
∴![]() 恒成立,
恒成立,
令![]() ,
,
∴![]() 对
对![]() ,
,![]() 恒成立,
恒成立,
∵![]() 在
在![]() 上单调递增,
上单调递增,
∴![]()
∴![]() ,
,
解得![]() ,
,
又![]() ,
,
∴![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】若一条直线与一个平面垂直,则称此直线与平面构成一个“正交线面对”.那么在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A. 48 B. 36 C. 24 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市大学生创业孵化基地某公司生产一种“儒风邹城”特色的旅游商品.该公司年固定成本为10万元,每生产千件需另投入2.7万元;设该公司年内共生产该旅游商品![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且满足函数关系:
万元,且满足函数关系: .
.
(Ⅰ)写出年利润![]() (万元)关于该旅游商品
(万元)关于该旅游商品![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在该旅游商品的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为![]() (
(![]() ,且
,且![]() );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
A. 每场比赛第一名得分![]() 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名
C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 及圆
及圆![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com