
分析 (1)根据双曲线的标准方程进行求解即可.
(2)根据复合命题真假关系得到p,q两命题应一真一假,进行求解即可.
解答 解:(1)由已知方程$\frac{x^2}{m+3}-\frac{y^2}{2m-1}=1$表示焦点在y轴上的双曲线,
则$\left\{\begin{array}{l}{m+3<0}\\{1-2m>0}\end{array}\right.$,得$\left\{\begin{array}{l}{m<-3}\\{m<\frac{1}{2}}\end{array}\right.$,得m<-3,即q:m<-3.
(2)若方程x2+2mx+(m+2)=0有两个不等的正根
则$\left\{{\begin{array}{l}{△=4{m^2}-4({m+2})>0}\\ \begin{array}{l}-2m>0\\ m+2>0\end{array}\end{array}}\right.$,解得-2<m<-1,即p:-2<m<-1.
因p或q为真,所以p、q至少有一个为真.
又p且q为假,所以p,q至少有一个为假.
因此,p,q两命题应一真一假,当p为真,q为假时,$\left\{{\begin{array}{l}{-2<m<-1}\\{m≥-3}\end{array}}\right.$,解得-2<m<-1;
当p为假,q为真时,$\left\{{\begin{array}{l}{m≤2或m≥-1}\\{m<-3}\end{array}}\right.$,解得m<-3.
综上,-2<m<-1或m<-3.
点评 本题主要考查复合命题的真假应用,根据条件求出命题为真命题的等价条件是解决本题的关键.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}{a^2}$ | B. | $\frac{1}{4}{a^2}$ | C. | $\frac{1}{8}{a^2}$ | D. | $\frac{{\sqrt{3}}}{8}{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
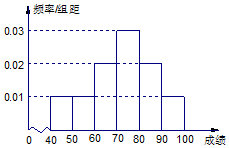 某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).
某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {-2,-1} | C. | {-2,-1} | D. | {-3,3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com