
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角的余弦值.
所成角的余弦值.
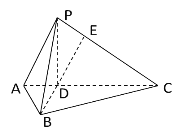
【答案】(1)见解析(2)![]()
【解析】
(1)要证明DE∥平面PAB,只需证DE与平面PAB内的一条直线平行即可.(2)由(1)知DE∥AP.则异面直线AB和DE所成角即AB和AP所成的角,由余弦定理计算即可.
(1)证明:∵AD=1,CD=2,![]()
∴在![]() 中,
中,![]() ∴DE∥AP.
∴DE∥AP.
∵AP平面PAB,DE平面PAB,
∴DE∥平面PAB;
(2)解:由(1)知DE∥AP.则异面直线AB和DE所成角即AB和AP所成的角.∵PD⊥AC,AD=1,PD=2,在![]() 中,AP2=AD2+PD2=12+22=5.
中,AP2=AD2+PD2=12+22=5.
∵BD⊥AC,AD=1,BD=1,在![]() 中,AB2=AD2+BD2=12+12=2.
中,AB2=AD2+BD2=12+12=2.
∵PD⊥BD,PD=2,在![]() 中,PB2=PD2+BD2=22+12=5.
中,PB2=PD2+BD2=22+12=5.
在![]() 中,cos∠PAB=
中,cos∠PAB= ![]() ,
,
∴异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召![]() 名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成
名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成![]() 组第
组第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,已知第
,得到的频率分布直方图如图所示,已知第![]() 组有
组有![]() 人.
人.

(1)求该组织的人数;
(2)若在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参加某社区的宣传活动,应从第
名志愿者参加某社区的宣传活动,应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第![]() 组至少有
组至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两所学校高三年级分别有600人,500人,为了解两所学校全体高三年级学生在该地区五校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 7 | 14 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 17 | x | 4 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 4 |
(1)计算x,y的值;
(2)若规定考试成绩在[120,150]内为优秀,由以上统计数据填写下面的2×2列联表,并判断是否有90%的把握认为两所学校的数学成绩有差异;
(3)若规定考试成绩在[120,150]内为优秀,现从已抽取的110人中抽取两人,要求每校抽1人,所抽的两人中有人优秀的条件下,求乙校被抽到的同学不是优秀的概率.
甲校 | 乙校 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k0) | 0.10 | 0.05 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若对于任意的
,若对于任意的![]() ,,当
,,当![]() 时,都有
时,都有![]() ,则称函数
,则称函数![]() 在
在![]() 上为非减函数.设函数
上为非减函数.设函数![]() 在
在![]() 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() ,则
,则![]() 等于( ).
等于( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)在(2,+∞)上单调递减,且y=f(x+2)为偶函数,则关于x的不等式f(2x﹣1)﹣f(x+1)>0的解集为( )
A.(﹣∞,﹣ ![]() )∪(2,+∞)
)∪(2,+∞)
B.(﹣ ![]() ,2)
,2)
C.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
D.( ![]() ,2)
,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,直线AP,AB,AD两两相互垂直,且AD∥BC,AP=AB=AD=2BC. 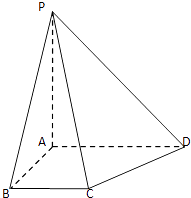
(1)求异面直线PC与BD所成角的余弦值;
(2)求钝二面角B﹣PC﹣D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com