

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源:不详 题型:解答题
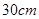 的
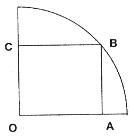
的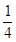 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长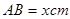 ,圆柱的体积为
,圆柱的体积为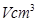 .
.
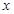 的函数关系式;
的函数关系式;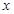 为何值时,才能使做出的圆柱形罐子体积V最大?
为何值时,才能使做出的圆柱形罐子体积V最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
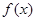 满足:①在x=1时有极值;②图像过点
满足:①在x=1时有极值;②图像过点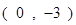 ,且在该点处的切线与直线
,且在该点处的切线与直线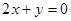 平行.
平行.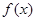 的解析式;
的解析式; 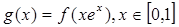 的值域;
的值域; 上任意两点的连线的斜率恒大于
上任意两点的连线的斜率恒大于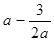 ,求
,求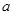 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
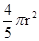 分,其中r(单位:cm)是瓶子的半径.已知每出售1ml的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为5cm.
分,其中r(单位:cm)是瓶子的半径.已知每出售1ml的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为5cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com