
【题目】某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.下图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知![]() ,历年中日泄流量在区间[30,60)
,历年中日泄流量在区间[30,60)
的年平均天数为156,一年按364天计.
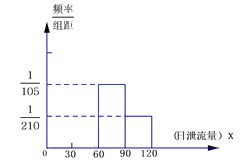
(Ⅰ)请把频率分布直方图补充完整;
(Ⅱ)该水电站希望安装的发电机尽可能运行,但每30万立方米的日泄流量才够运行一台发电机,如![]() 时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
【答案】(Ⅰ)见解析;(Ⅱ)要使水电站日利润的期望值最大,该水电站应安装3台发电机.
【解析】试题分析:(Ⅰ)可利用频率分布直方图的性质,补全图像;
(Ⅱ)分别计算安装1台,2台,3台的日利润的期望值,然后进行比较.
试题解析:
(Ⅰ)在区间[30,60)的频率为![]()
![]() ,
,
设在区间[0,30)上, ![]() ,
,
则![]() ,
,
解得![]() ,
,
补充频率分布直方图如图;
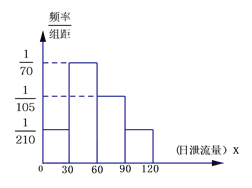
(Ⅱ)记水电站日利润为Y元.由(Ⅰ)知:不能运行发电机的概率为![]() ,恰好运行一台发电机的概率为
,恰好运行一台发电机的概率为![]() ,恰好运行二台发电机的概率为
,恰好运行二台发电机的概率为![]() ,恰好运行三台发电机的概率为
,恰好运行三台发电机的概率为![]() ,
,
①若安装1台发电机,则Y的值为-500,4000,其分布列为
Y | -500 | 4000 |
P |
|
|
E(Y)=![]() ;
;
②若安装2台发电机,则Y的值为-1000,3500,8000,其分布列为
Y | -1000 | 3500 | 8000 |
P |
|
|
|
E(Y)=![]() ;
;
③若安装3台发电机,则Y的值为-1500,3000,7500,12000,其分布列为
Y | -1500 | 3000 | 7500 | 12000 |
P |
|
|
|
|
E(Y)=![]() ;
;
∵![]()
∴要使水电站日利润的期望值最大,该水电站应安装3台发电机.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() 在
在![]() 上存在极值点,求
上存在极值点,求![]() 的取值范围;
的取值范围;
(2)设![]() ,
, ![]() ,若
,若![]() 存在最大值,记为
存在最大值,记为![]() ,则当
,则当![]() 时,
时, ![]() 是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究一种昆虫的产卵数![]() 和温度
和温度![]() 是否有关,现收集了7组观测数据列于下表中,并作出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈线性相关关系,现分别用模型①:
是否有关,现收集了7组观测数据列于下表中,并作出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈线性相关关系,现分别用模型①:![]() 与模型②:
与模型②:![]() 作为产卵数
作为产卵数![]() 和温度
和温度![]() 的回归方程来建立两个变量之间的关系.
的回归方程来建立两个变量之间的关系.
温度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
|
|
|
|
26 | 692 | 80 | 3.57 |
|
|
|
|
1157.54 | 0.43 | 0.32 | 0.00012 |
其中![]() ,
, ![]()
![]() ,
, ![]() ,
,
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ,
, ![]() .
.

(1)在答题卡中分别画出![]() 关于
关于![]() 的散点图、
的散点图、![]() 关于
关于![]() 的散点图,根据散点图判断哪一个模型更适宜作为回归方程类型?(给出判断即可,不必说明理由).
的散点图,根据散点图判断哪一个模型更适宜作为回归方程类型?(给出判断即可,不必说明理由).

(2)根据表中数据,分别建立两个模型下建立![]() 关于
关于![]() 的回归方程;并在两个模型下分别估计温度为
的回归方程;并在两个模型下分别估计温度为![]() 时的产卵数.(
时的产卵数.(![]() 与估计值均精确到小数点后两位)(参考数据:
与估计值均精确到小数点后两位)(参考数据: ![]() ,
, ![]() ,
, ![]() )
)
(3)若模型①、②的相关指数计算得分分别为![]() ,
, ![]() ,请根据相关指数判断哪个模型的拟合效果更好.
,请根据相关指数判断哪个模型的拟合效果更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 如果平面![]() 外的直线
外的直线![]() 不平行于平面
不平行于平面![]() ,则平面
,则平面![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
B. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么直线
,那么直线![]() 平面
平面![]()
C. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为2的正三角形.
是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com