
【题目】在数列![]() 中,
中,![]() ,若
,若![]() (
(![]() 为常数),则称
为常数),则称![]() 为“等差比数列”.下列是对“等差比数列”的判断:
为“等差比数列”.下列是对“等差比数列”的判断:
①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列;
;②等差数列一定是等差比数列;
③等比数列一定是等差比数列;④等差比数列中可以有无数项为![]() .
.
其中正确的判断是( ).
A.①②B.②③C.③④D.①④
科目:高中数学 来源: 题型:
【题目】如果执行程序框图,输入正整数![]() ,
,![]() ,满足
,满足![]() ,那么输出的
,那么输出的![]() 等于( ).
等于( ).
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/25/2492401463009280/2492946029182977/STEM/3a3c20c7c34c41528daf48813411739a.png]
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线![]() 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD与△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①![]() ;
;
②∠BAC=60°;
③三棱锥D﹣ABC是正三棱锥;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确结论的序号是 .(请把正确结论的序号都填上)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到一瓶已过保质期的概率为 _________ .(结果用最简分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() (
(![]() 是常数,且
是常数,且![]() ),
),![]()
![]() ,数列
,数列![]() 的首项
的首项![]() ,
,![]()
![]() .
.
(1)证明:![]() 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)当![]() 时,求数列
时,求数列![]() 的最小项.
的最小项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某段城铁线路上依次有![]() 、
、![]() 、
、![]() 三站,
三站,![]() ,
,![]() ,在列车运行时刻表上,规定列车
,在列车运行时刻表上,规定列车![]() 时整从
时整从![]() 站出发,
站出发,![]() 时
时![]() 分到达
分到达![]() 站并停车
站并停车![]() ,
,![]() 时
时![]() 分到达
分到达![]() 站,在实际运行时,假设列车从
站,在实际运行时,假设列车从![]() 站正点出发,在
站正点出发,在![]() 站停留
站停留![]() ,并在行驶时以同一速度
,并在行驶时以同一速度![]() 匀速行驶,列车从
匀速行驶,列车从![]() 站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(1)分别写出列车在![]() 、
、![]() 两站的运行误差;
两站的运行误差;
(2)若要求列车在![]() 、
、![]() 两站的运行误差之和不超过
两站的运行误差之和不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比,药物释放完毕后,
成正比,药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).如图所示,根据图中提供的信息,回答下列问题:
为常数).如图所示,根据图中提供的信息,回答下列问题:
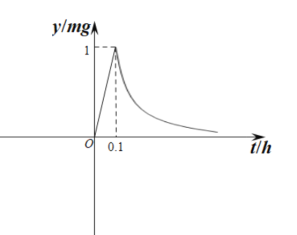
(1)从药物释放开始,每立方米空气中的含药量![]() 与时间
与时间![]() 之间的函数关系式为________;
之间的函数关系式为________;
(2)据测定,当空气中每立方米的含药量降低到![]() 以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com