
在平面直角坐标系xOy中,设曲线C1: 所围成的封闭图形的面积为
所围成的封闭图形的面积为
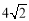 ,曲线C1上的点到原点O的最短距离为
,曲线C1上的点到原点O的最短距离为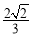 .以曲线C1与坐标轴的交点为顶点的椭圆记
.以曲线C1与坐标轴的交点为顶点的椭圆记
为C2.
(1)求椭圆C2的标准方程;
(2)设AB是过椭圆C2中心O的任意弦,l是线段AB的垂直平分线.M是l上的点(与O不重合).
①若MO=2OA,当点A在椭圆C2上运动时,求点M的轨迹方程;
②若M是l与椭圆C2的交点,求△AMB的面积的最小值.
(1)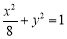 ;(2)①
;(2)①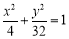 ;②
;②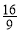 .
.
【解析】
试题分析:(1)对于曲线C1: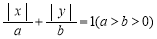 的处理,关键问题是两个绝对值的处理,根据x,y的特点,不难发现与坐标系中的四个象限有关,进而即可得到
的处理,关键问题是两个绝对值的处理,根据x,y的特点,不难发现与坐标系中的四个象限有关,进而即可得到 ,即可得出椭圆方程; (2)①由l是线段AB的垂直平分线,可转化为:
,即可得出椭圆方程; (2)①由l是线段AB的垂直平分线,可转化为: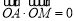 ,又由MO=2OA,可转化得到:
,又由MO=2OA,可转化得到: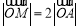 ,这样的好处是两条件均转化为向量了,设出点M和点A的坐标即可得到关系:
,这样的好处是两条件均转化为向量了,设出点M和点A的坐标即可得到关系: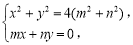 解出
解出 再利用点M在所求椭圆上即可求出:
再利用点M在所求椭圆上即可求出: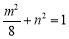 ;②中要求△AMB的面积的最小值,根据此地三角形的特点,不难想到直线AB的设出,根据斜率是否存在,可先考虑两种特殊情况:一种不存在;另一种为0,再考虑一般情形,运用方程组思想即可得:
;②中要求△AMB的面积的最小值,根据此地三角形的特点,不难想到直线AB的设出,根据斜率是否存在,可先考虑两种特殊情况:一种不存在;另一种为0,再考虑一般情形,运用方程组思想即可得: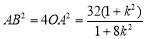 和
和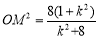 ,进而表示出面积:
,进而表示出面积: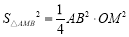 ,最后结合不等式知识即可求出最小值.
,最后结合不等式知识即可求出最小值.
试题解析:(1)由题意得 又
又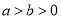 ,解得
,解得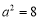 ,
,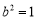 .
.
因此所求椭圆的标准方程为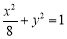 . 4分
. 4分
(2)①设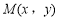 ,
,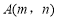 ,则由题设知:
,则由题设知: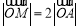 ,
,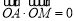 .
.
即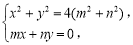 解得
解得 8分
8分
因为点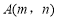 在椭圆C2上,所以
在椭圆C2上,所以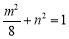 ,
,
即 ,亦即
,亦即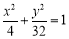 .
.
所以点M的轨迹方程为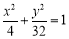 . 10分
. 10分
②假设AB所在的直线斜率存在且不为零,设AB所在直线方程为y=kx(k≠0).
解方程组 得
得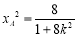 ,
,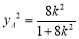 ,
,
所以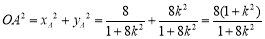 ,
,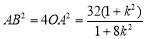 .
.
又 解得
解得 ,
,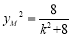 ,所以
,所以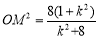 . 12分
. 12分
由于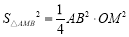
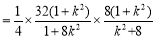
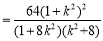

 ,
,
当且仅当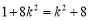 时等号成立,即k=±1时等号成立,
时等号成立,即k=±1时等号成立,
此时△AMB面积的最小值是S△AMB=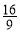 . 15分
. 15分
当k=0,S△AMB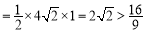 ;
;
当k不存在时,S△AMB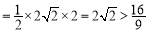 .
.
综上所述,△AMB面积的最小值为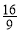 . 16分
. 16分
考点:1.椭圆方程;2.直线与椭圆的位置关系;3.基本不等式


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷(解析版) 题型:填空题
一个正方体玩具的6个面分别标有数字1,2,2,3,3,3.若连续抛掷该玩具两次,则向上一面数字之和为5的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试文科数学试卷(解析版) 题型:填空题
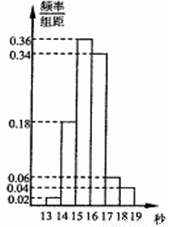
某学校为了解该校600名男生的百米成绩(单位:s),随机选择了50名学生进行调查,
下图是这50名学生百米成绩的频率分布直方图。根据样本的频率分布,估计这600名学生中成绩在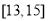 (单位:s)内的人数大约是 .
(单位:s)内的人数大约是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,设动点P,Q都在曲线C: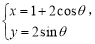 (θ为参数)上,且这两点对应的参数分别为θ=α与θ=2α(0<α<2π),设PQ的中点M与定点A(1,0)间的距离为d,求d的取值范围.
(θ为参数)上,且这两点对应的参数分别为θ=α与θ=2α(0<α<2π),设PQ的中点M与定点A(1,0)间的距离为d,求d的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:填空题
若不等式(mx-1)[3m 2-( x + 1)m-1]≥0对任意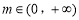 恒成立,则实数x的值为 .
恒成立,则实数x的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
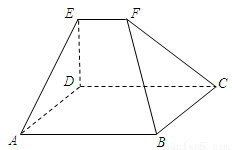
(1)求证:AB∥EF;
(2)求证:平面BCF⊥平面CDEF.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
已知a,b是不相等的正数,在a,b之间分别插入m个正数a1,a2, ,am和正数b1,b2, ,
bm,使a,a1,a2, ,am,b是等差数列,a,b1,b2, ,bm,b是等比数列.
(1)若m=5,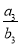 =
=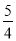 ,求
,求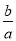 的值;
的值;
(2)若b=λa(λ∈N*,λ≥2),如果存在n (n∈N*,6≤n≤m)使得an-5=bn,求λ的最小值及此时m的值;
(3)求证:an>bn(n∈N*,n≤m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com