在三角形ABC中,a,b,c分别表示三内角A、B、C所对的边的长,且lgsinA,lgsinB,lgsinC成等差数列;直线xsin2A+ysinA-a=0与xsin2B+ysinC-c=0的位置关系是( )
A.重合
B.相交但不平行
C.垂直
D.平行
【答案】
分析:由查等差数列的定义 可得sin
2B=sinA•sinC,求出两直线的斜率和它们在y轴上的截距,发现斜率相等,利用正弦定理可得它们在y轴上的截距也相等,从而得到两直线重合.
解答:解:∵lg
sinA,lg
sinB,lg
sinC成等差数列,∴2lg
sinB =lg
sinA +lg
sinC ,
∴sin
2B=sinA•sinC. 直线xsin
2A+ysinA-a=0的斜率为-sinA,xsin
2B+ysinC-c=0 的斜率为-
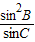
,
∴这两直线的斜率相等.它们在y轴上的截距分别为
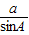
和
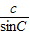
,由正弦定理知,它们在y轴上的截距也相等,
故两直线重合,
故选A.
点评:本题考查等差数列的定义,直线和直线的位置关系,正弦定理的应用,求出两直线的斜率和它们在y轴上的截距,是解题的关键.

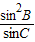 ,
,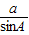 和
和 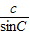 ,由正弦定理知,它们在y轴上的截距也相等,
,由正弦定理知,它们在y轴上的截距也相等,
