【答案】
分析:(1)分别令x
1=x
2=0,x
1=1,x
2=0,f(x
)=f(1),又因为f(x)为单调函数,从而可求x
的值;
(2)由(1)得f(x
1+x
2)=f(x
1)+f(x
2)+1,令x
1=n,x
2=1,f(n+1)=f(n)+f(1)+1=f(n)+2,f(n)=2n-1.故可求a
n进而可有
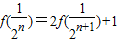
,从而可求通项,故可证;
(3)构造函数F(n)=a
n+1+a
n+2+…+a
2n,证明n≥2时,为单调减函数,从而可求x的取值范围.
解答:解:(1)令x
1=x
2=0⇒f(x
)=-f(0).又令x
1=1,x
2=0,f(1)=-f(0).
∴f(x
)=f(1),由函数f(x)单调性知,x
=1.
(2)由(1)知,f(x
1+x
2)=f(x
1)+f(x
2)+f(1)=f(x
1)+f(x
2)+1,
由x
1,x
2的任意性,令x
1=n,x
2=1,f(n+1)=f(n)+f(1)+1=f(n)+2,
∴f(n)=2n-1.(n∈N
*).
∴
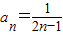
.
又∵
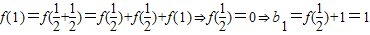
.
又∵
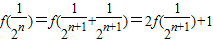
,
∴
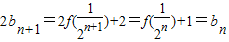
.
∴
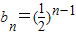
.
由数列求和方法知:
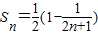
,
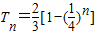
.∴
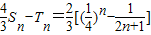
.
∵4
n=(3+1)
n=C
nn3
n+C
nn-13
n-1+…+C
n13+C
n≥3n+1>2n+1,∴

.
(3)令F(n)=a
n+1+a
n+2+…+a
2n⇒F(n+1)-F(n)=a
2n+1+a
2n+2-a
n+1=
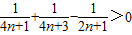
(通分易证)∴当n≥2时,
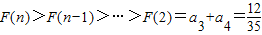
.
∴
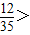
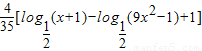
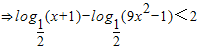
.
解此不等式,所以x的取值范围为
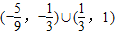
.
点评:本题以新定义为载体,考查抽象函数,考查赋值法,同时考查构造函数,利用函数的单调性解决恒成立问题.

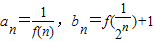 ,记Sn=a1a2+a2a3+…+anan+1,Tn=b1b2+b2b3+…+bnbn+1,比较
,记Sn=a1a2+a2a3+…+anan+1,Tn=b1b2+b2b3+…+bnbn+1,比较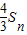 与Tn的大小关系,并给出证明;
与Tn的大小关系,并给出证明;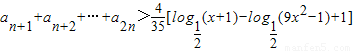 对任意不小于2的正整数n都成立,求x的取值范围.
对任意不小于2的正整数n都成立,求x的取值范围.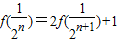 ,从而可求通项,故可证;
,从而可求通项,故可证;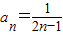 .
.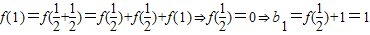 .
.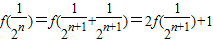 ,
,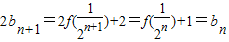 .
.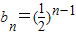 .
.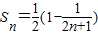 ,
,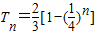 .∴
.∴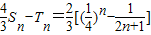 .
. .
.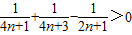 (通分易证)∴当n≥2时,
(通分易证)∴当n≥2时,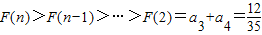 .
.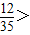
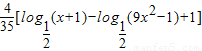
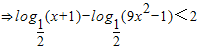 .
.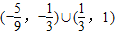 .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案