
【题目】已知A,B是椭圆 ![]() =1和双曲线
=1和双曲线 ![]() =1的公共顶点,其中a>b>0,P是双曲线上的动点,M是椭圆上的动点(P,M都异于A,B),且满足
=1的公共顶点,其中a>b>0,P是双曲线上的动点,M是椭圆上的动点(P,M都异于A,B),且满足 ![]() =λ(
=λ( ![]() )(λ∈R),设直线AP,BP,AM,BM的斜率分别为k1 , k2 , k3 , k4 , 若k1+k2=
)(λ∈R),设直线AP,BP,AM,BM的斜率分别为k1 , k2 , k3 , k4 , 若k1+k2= ![]() ,则k3+k4= .
,则k3+k4= .
科目:高中数学 来源: 题型:
【题目】如图所示的是自动通风设施![]() 该设施的下部ABCD是等腰梯形,其中
该设施的下部ABCD是等腰梯形,其中![]() 米,高
米,高![]() 米,
米,![]() 米
米![]() 上部CmD是个半圆,固定点E为CD的中点
上部CmD是个半圆,固定点E为CD的中点![]() 是由电脑控制其形状变化的三角通风窗
是由电脑控制其形状变化的三角通风窗![]() 阴影部分均不通风
阴影部分均不通风![]() ,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
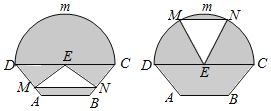
![]() 设MN与AB之间的距离为x米,试将三角通风窗
设MN与AB之间的距离为x米,试将三角通风窗![]() 的通风面积
的通风面积![]() 平方米
平方米![]() 表示成关于x的函数
表示成关于x的函数![]() ;
;
![]() 当MN与AB之间的距离为多少米时,三角通风窗
当MN与AB之间的距离为多少米时,三角通风窗![]() 的通风面积最大?求出这个最大面积.
的通风面积最大?求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合M={1,2…9}中抽取3个不同的数构成集合{a1 , a2 , a3}
(1)对任意i≠j,求满足|ai﹣aj|≥2的概率;
(2)若a1 , a2 , a3成等差数列,设公差为ξ(ξ>0),求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率.
斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
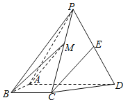
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系xOy中,直线l的参数方程为 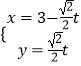 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程和直线l普通方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(3,0),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校青年职工、中年职工、老年职工的人数之比为7:5:3,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 .若样本中的青年职工为14人,则样本容量为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com