
分析 令f(x)=0,判断得到a>0,利用绝对值的代数意义化简,得到两个一元二次方程,由f(x)的零点个数为3,得到两方程共有3个解,即一个方程△>0,一个方程△=0,即可求出a的值.
解答 解:令f(x)=0,得到|4x-x2|-a=0,即|4x-x2|=a,
可得4x-x2=a或4x-x2=-a,
即x2-4x+a=0或x2-4x-a=0,
若a=0,解得:x=0或x=4,只有两个解,舍去,
∴a>0,
由f(x)的零点个数为3,得到两方程共有3个解,即一个方程△>0,一个方程△=0,
若x2-4x+a=0中的△=16-4a>0,即a<4;x2-4x-a=0的△=16+4a=0,即a=-4,不合题意,舍去;
若x2-4x+a=0中的△=16-4a=0,即a=4;x2-4x-a=0的△=16+4a>0,即a>-4,满足题意,
则a=4,
故答案为:4
点评 此题考查了函数零点的判定定理,以及一元二次方程根的判别式,函数的零点的研究就可转化为相应方程根的问题,函数与方程的思想得到了很好的体现.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
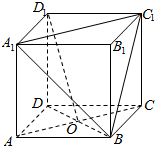 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x | B. | x2=-4y | C. | x2+4y2=1 | D. | x2-4y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com