分析:(1)由四棱柱的结构牲,可得AC是A1C在平面ABCD上的射影,及AC⊥BD,由三垂线定理可得BD⊥A1C;
(2)连接A1E,C1E,我们根据二面角的定义可得∠A1EC1为二面角A1-BD-C1的平面角,解△A1EC1,即可求出二面角A1-BD-C1的大小;
( 3)过B作BF∥AD交CD于F,则∠FBC1为异面直线AD与BC所成角,解Rt△BCF,即可求出异面直线AD与BC所成角的余弦值.
解答:解:(1)∵棱柱ABCD-A
1B
1C
1D
1为直四棱柱,
∴AA
1⊥平面ABCD,
又AB=AD,CB=CD,
故△ABC≌△ADC
则∠BAC=∠DAC
故AE为等腰△BAD中顶角的角平分线
故AE⊥BD
即AC⊥BD,AC是A
1C在平面ABCD上的射影,由三垂线定理知A
1C⊥BD …(4分)
(2)连接A
1E,C
1E,
∵E为AC与BD的交点且AC⊥BD,
∴A
1E⊥BD,C
1E⊥BD,
∴∠A
1EC
1为二面角A
1-BD-C
1的平面角,…(6分)
∵AB⊥BC,
∴AD⊥DC,
∴∠A
1D
1C
1=∠ADC=90°,
又∵A
1D
1=AD=2,D
1C
1=DC=2
,A
1A=
,AC⊥BD,
∴A
1C
1=4,AE=1,EC=3,
∴A
1E=2,C
1E=2
,
在△A
1EC
1中,A
1C
12=A
1E
2+C
1E
2,
∴∠A
1EC
1=90°,
∴二面角A
1-BD-C
1为90° …(10分)
( 3)∵AD⊥DC,
∴AD⊥平面CD
1,过B作BF∥AD交CD于F,
则∠FBC
1为所求的角,BF⊥平面CD
1,
∵AD=AB=2,AD⊥DC,AC⊥BD,
∴CD=CB=2
,
∴∠BCD=60°,
在Rt△BCF中,BF=BCsin60°=3,
∵BC
1=
,
∴cos∠FBC
1=
=
∴异面直线AD与BC所成角的余弦值为
…(14分)
点评:本题考查的知识点是二面角的平面角及求法,异面直线及其所在的角,其中(1)的关键是引入三垂线定理证明线面垂直;(2)的关键是确定∠A1EC1为二面角A1-BD-C1的平面角,(3)的关键是确定∠FBC1为异面直线AD与BC所成角.

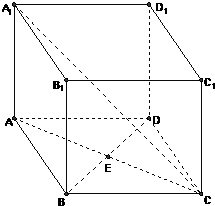 如图,直四棱柱ABCD-A1B1C1D1中,AB=AD=2,CB=CD=2
如图,直四棱柱ABCD-A1B1C1D1中,AB=AD=2,CB=CD=2 

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.