
【题目】某校为了了解学生对电子竞技的兴趣,从该校高二年级的学生中随机抽取了![]() 人进行检查,已知这
人进行检查,已知这![]() 人中有
人中有![]() 名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有
名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有![]() 的人对电子竞技有兴趣.
的人对电子竞技有兴趣.
![]() 在被抽取的女生中与
在被抽取的女生中与![]() 名高二
名高二![]() 班的学生,其中有
班的学生,其中有![]() 名女生对电子产品竞技有兴趣,先从这
名女生对电子产品竞技有兴趣,先从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求其中至少有
人,求其中至少有![]() 人对电子竞技有兴趣的概率;
人对电子竞技有兴趣的概率;
![]() 完成下面的
完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“电子竞技的兴趣与性别有关”.
的把握认为“电子竞技的兴趣与性别有关”.
有兴趣 | 没兴趣 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考数据:
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
参考公式:
【答案】![]()
![]() ;
;![]() 列联表见解析,没有.
列联表见解析,没有.
【解析】
(1)计算出从![]() 名学生中随机抽取
名学生中随机抽取![]() 人的可能,再计算出抽到的
人的可能,再计算出抽到的![]() 人中至少有
人中至少有![]() 人对电子竞技有兴趣的可能,利用古典概型公式即得答案;
人对电子竞技有兴趣的可能,利用古典概型公式即得答案;
(2)先填写列联表,然后计算![]() ,与
,与![]() 比较大小即可得到答案.
比较大小即可得到答案.
![]() 从
从![]() 名学生中随机抽取
名学生中随机抽取![]() 人,共有
人,共有![]() 种不同的抽取方案;抽到的
种不同的抽取方案;抽到的![]() 人中至少有
人中至少有![]() 人对电子竞技有兴趣的方案数有:
人对电子竞技有兴趣的方案数有:![]() 种
种
![]() 抽取
抽取![]() 人中至少有
人中至少有![]() 人对电子竞技有兴趣的概率为
人对电子竞技有兴趣的概率为![]() .
.
![]() 设对电子竞技没兴趣的学生人数为
设对电子竞技没兴趣的学生人数为![]() ,
,
![]() 对电子竞技没兴趣的学生人数与对电子竞技有兴趣的女生人数一样多
对电子竞技没兴趣的学生人数与对电子竞技有兴趣的女生人数一样多
由题![]() ,解得
,解得![]() .
.
又女生中有![]() 的人对电子竞技有兴趣,
的人对电子竞技有兴趣,
![]() 女生人数为
女生人数为![]()
男生人数为![]() ,其中有
,其中有![]() 人对电子竞技没兴趣
人对电子竞技没兴趣
得到下面列联表

![]()
![]() 没用
没用![]() 的把握认为“对电子竞技的兴趣与性别有关”.
的把握认为“对电子竞技的兴趣与性别有关”.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同零点,是否存在实数
的两个不同零点,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数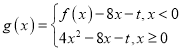 ,存在
,存在![]() 个零点.
个零点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设![]() 分别是这
分别是这![]() 个零点中的最小值与最大值,求
个零点中的最小值与最大值,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校将甲、乙等6名新招聘的老师分配到4个不同的年级,每个年级至少分配1名教师,且甲、乙两名老师必须分到同一个年级,则不同的分法种数为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数![]() (千人)与时间
(千人)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() ),人均消费
),人均消费![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]()
(1)求该商场的日收益![]() (千元)与时间
(千元)与时间![]() (天)(
(天)(![]() ,
, ![]() )的函数关系式;
)的函数关系式;
(2)求该商场日收益的最小值(千元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足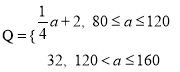 ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校参加夏令营的同学有3名男同学![]() 和3名女同学
和3名女同学![]() ,其所属年级情况如下表:
,其所属年级情况如下表:
高一年级 | 高二年级 | 高三三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母写出这个试验的样本空间;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件![]() 的样本点,并求事件
的样本点,并求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有![]() 四辆汽车,其中
四辆汽车,其中![]() 车的车牌尾号为0,
车的车牌尾号为0,![]() 两辆车的车牌尾号为6,
两辆车的车牌尾号为6,![]() 车的车牌尾号为5,已知在非限行日,每辆车都有可能出车或不出车.已知
车的车牌尾号为5,已知在非限行日,每辆车都有可能出车或不出车.已知![]() 两辆汽车每天出车的概率为
两辆汽车每天出车的概率为![]() ,
,![]() 两辆汽车每天出车的概率为
两辆汽车每天出车的概率为![]() ,且四辆汽车是否出车是相互独立的.
,且四辆汽车是否出车是相互独立的.
该公司所在地区汽车限行规定如下:

(1)求该公司在星期四至少有2辆汽车出车的概率;
(2)设![]() 表示该公司在星期一和星期二两天出车的车辆数之和,求
表示该公司在星期一和星期二两天出车的车辆数之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com