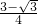
16π [-2,4]
分析:A:先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ
2=x
2+y
2,将曲线的极坐标方程化成直角坐标方程,再利用直角坐标中点的坐标、直线的方程求解成的图形的面积即可.
B:连接辅助线,根据圆周角是30°,得到对应的圆心角是60°,根据圆的半径相等,得到三角形是一个等边三角形,求出半径的长度,根据圆的面积公式,得到结果.
解答:
解:A:曲线ρcosθ+ρsinθ=1的直角坐标方程分别为:
x+y-1=0.它与x轴的交点为B(1,0).
曲线θ=

的直角坐标方程分别为:

x-y=0.
它们的交点坐标为A(
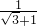
,
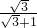
),
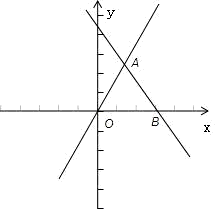
∴由三条曲线
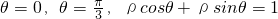
围成的图形如图所示.
∴S=

OB×h=

×1×
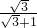
=
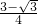
.
故答案为:
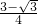
.
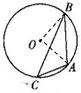
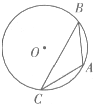
B:解:连接OA,OB,
∵∠ACB=30°,
∴∠AoB=60°,
∴△AOB是一个等边三角形,
∴OA=AB=4,
∴⊙O的面积是16π
故答案为16π.
点评:A:本小题考查简单曲线的极坐标方程、点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
B:本小题考查圆周角的性质,考查等边三角形,考查圆的面积,是一个等边三角形,在解题时主要做法是构造等边三角形.

 A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ=
A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ= ,ρcosθ+ρsinθ=1围成图形的面积是________.
,ρcosθ+ρsinθ=1围成图形的面积是________.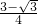 16π [-2,4]
16π [-2,4] 解:A:曲线ρcosθ+ρsinθ=1的直角坐标方程分别为:
解:A:曲线ρcosθ+ρsinθ=1的直角坐标方程分别为: 的直角坐标方程分别为:
的直角坐标方程分别为: x-y=0.
x-y=0.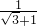 ,
,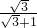 ),
),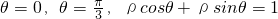 围成的图形如图所示.
围成的图形如图所示. OB×h=
OB×h= ×1×
×1×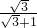 =
=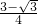 .
.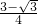 .
. B:解:连接OA,OB,
B:解:连接OA,OB,

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案 A.(坐标系与参数方程选做题)在极坐标系中,点P(2,
A.(坐标系与参数方程选做题)在极坐标系中,点P(2, 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)
(考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分) (2010•陕西一模)(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(2010•陕西一模)(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)