
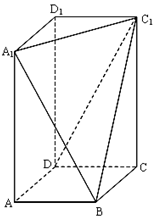
 已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.
已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.分析 (1)根据长方体的体积减去切除的三棱锥的体积=几何体的体积,求出A1A的长度,求解各平面的面积可得几何体ABCD-A1C1D1的表面积;
(2)在平面CC1D1D中作D1Q⊥C1D交C1C于Q,过Q作QP∥CB交BC1于点P,则A1P⊥C1D,证明C1D⊥PA1,利用△C1D1Q∽△CC1D,求C1Q=1,证明四边形PQ1A1为直角梯形,运用勾股定理求线段A1P的长.
解答 解:(1)根据长方体的体积减去切除的三棱锥的体积=几何体的体积,即${V}_{ABCD-{{A}_{1}B}_{1}{C}_{1}}={V}_{A{C}_{1}}-{V}_{B-A{B}_{1}{C}_{1}}$=$2×2×A{A}_{1}-\frac{1}{3}×\frac{1}{2}×2×2×A{A}_{1}=\frac{10}{3}A{A}_{1}$=$\frac{40}{3}$,
∴AA1=4
∴A1B=C1B=2$\sqrt{5}$,A1C1=$2\sqrt{2}$,设A1C1D1的中点H,
则BH=$3\sqrt{2}$.
∴${S}_{△{A}_{1}B{C}_{1}}$=$\frac{1}{2}×2\sqrt{2}×3\sqrt{2}=6$
几何体ABCD-A1C1D1的表面积S=3×8+4+2+6=36.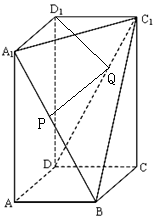
(2)在平面CC1D1D中作D1Q⊥C1D交C1C于Q,
过Q作QP∥CB交BC1于点P,则A1P⊥C1D.
∵A1D1⊥平面CC1D1D,C1D1?平面CC1D1
∴A1D1⊥C1D,
而QP∥CB,A1D1∥CB,∴QP∥A1D1
又∵A1D1∩QD1
∴C1D⊥平面PQC1A1
∵C1D?平面PQC1A1且PA1?平面PQC1A1,
∴C1D⊥PA1
∵△C1D1Q∽△CC1D,
∴$\frac{{C}_{1}Q}{CD}=\frac{{{D}_{1}C}_{1}}{{C}_{1}C}$,
∴C1Q=1,
又∵QP∥CB,
∴QP=$\frac{1}{4}$CB=$\frac{1}{2}$
∴四边形PQD1A1为直角梯形,且高D1Q=$\sqrt{5}$.
∴PA1=$\sqrt{(2-\frac{1}{2})^{2}+5}=\frac{\sqrt{29}}{2}$.
故得点P在线段BC1上,且A1P⊥C1D,线段A1P的长为$\frac{\sqrt{29}}{2}$.
点评 本题考查了立体几何的体积计算,考查了线面、面面平行,线面、面面垂直等简单的立体几何知识,考查学生对书本知识的掌握情况以及空间想象、推理能力,是中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.
如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:3 | B. | 1 | C. | 5:3 | D. | 3:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
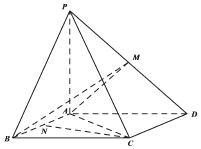 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com