
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
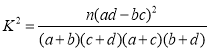 ,其中
,其中![]() .
.
【答案】(1)表格见解析;(2)有99.9%的把握认为学习积极性高与参加文体活动有关,理由见解析;(3)![]()
【解析】
(1)计算学习积极性不高的有![]() 人,完善列联表得到答案.
人,完善列联表得到答案.
(2)![]() ,对比临界值表得到答案.
,对比临界值表得到答案.
(3)有2人学习积极性高,设为![]() 、
、![]() ,有3人学习积极性不高,设为
,有3人学习积极性不高,设为![]() 、
、![]() 、
、![]() ,列出所有情况,统计满足条件的情况,得到概率.
,列出所有情况,统计满足条件的情况,得到概率.
(1)根据题意,全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() ,
,
则学习积极性不高的有![]() 人,
人,
据此可得:列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | 40 | 120 |
学习积极性不高 | 20 | 60 | 80 |
合计 | 100 | 100 | 200 |
(2)根据题意,由列联表可得:![]() ;
;
故有99.9%的把握认为学习积极性高与参加文体活动有关;
(3)根据题意,从不参加文体活动的同学中按照分层抽样的方法选取5人,有2人学习积极性高,设为![]() 、
、![]() ,有3人学习积极性不高,设为
,有3人学习积极性不高,设为![]() 、
、![]() 、
、![]() ,从中选取2人,
,从中选取2人,
有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共10种情况,
,共10种情况,
其中至少有1人学习积极性不高的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共9种情况,
,共9种情况,
至少有1人学习积极性不高的概率![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为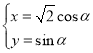 (
(![]() 为参数).在以
为参数).在以![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:在平面四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如图1),若将
(如图1),若将![]() 沿对角线BD折叠,使
沿对角线BD折叠,使![]() (如图2).请在图2中解答下列问题.
(如图2).请在图2中解答下列问题.
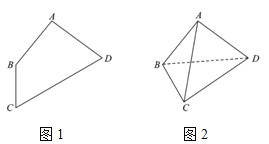
(1)证明:![]() ;
;
(2)求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一个圆分成n(n≥2)个扇形,依次记为![]() ,每一扇形都可用红、白、蓝三种不同颜色的任一种涂色,要求相邻的扇形的颜色互不相同,问有多少种涂色法?
,每一扇形都可用红、白、蓝三种不同颜色的任一种涂色,要求相邻的扇形的颜色互不相同,问有多少种涂色法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半(即
是偶数,就将它减半(即![]() );如果
);如果![]() 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即![]() ),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数![]() (首项)按照上述规则施行变换后的第6项为1(注:1可以多次出现),则
(首项)按照上述规则施行变换后的第6项为1(注:1可以多次出现),则![]() 的所有不同值的个数为( )
的所有不同值的个数为( )
A.3B.4C.5D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足![]() an+1
an+1![]() an=0(n∈N*),且
an=0(n∈N*),且![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求数列{an}的通项公式;
(2)令bn=![]() (n∈N*),求数列{bn}的前n项和为
(n∈N*),求数列{bn}的前n项和为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线C相交于A,B两点,与圆
与抛物线C相交于A,B两点,与圆![]() 相交于D,E两点,O为坐标原点,
相交于D,E两点,O为坐标原点,![]() ,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com