
【题目】设非空集合s={x|m≤x≤l}满足:当x∈S时,有y=x2∈S.给出如下三个命题:
①若m=1,则S={1};
②若m=﹣ ![]() ,则
,则 ![]() ≤l≤1;
≤l≤1;
③若l= ![]() ,则﹣
,则﹣ ![]() ≤m≤0.
≤m≤0.
④若l=1,则﹣1≤m≤0或m=1.
其中正确命题的是 .
【答案】①②③④
【解析】解:由定义设非空集合S={x|m≤x≤l}满足:当x∈S时,有y=x2∈S可知:符合定义的参数m的值一定大于等于﹣1,符合条件的l的值一定大于等于0,小于等于1,
如此才能保证l∈S时,有l2∈S即l2≤l,再对各个命题进行判断:
对于①m=1,m2=1∈S故必有 ![]() ,可得l=1,S={1},故正确;
,可得l=1,S={1},故正确;
②m=﹣ ![]() ,
, ![]() 则
则 ![]() ,解得
,解得 ![]() ≤l≤1,故正确;
≤l≤1,故正确;
③若l= ![]() ,则
,则 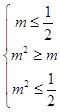 ,可解得﹣
,可解得﹣ ![]() ≤m≤0,故正确;
≤m≤0,故正确;
④若l=1,则 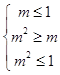 可解得﹣1≤m≤0或m=1,故正确.
可解得﹣1≤m≤0或m=1,故正确.
所以答案是:①②③④
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


科目:高中数学 来源: 题型:
【题目】(文)已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[﹣3,3],且它们在x∈[0,3]上的图象如图所示,则不等式 ![]() 的解集是
的解集是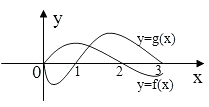
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 为
为![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2ax+b , 且 ![]() ,
, ![]() .
.
(Ⅰ)求实数a,b的值并判断函数f(x)的奇偶性;
(Ⅱ)判断函数f(x)在[0,+∞)上的单调性,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( ) 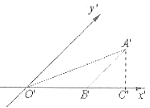
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①已知M={(x,y)| ![]() =3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=﹣6;
=3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=﹣6;
②已知点A(x1 , y1),B(x2 , y2),则以AB为直径的圆的方程是(x﹣x1)(x﹣x2)+(y﹣y1)(y﹣y2)=0;
③ ![]() =1(a≠b)表示焦点在x轴上的椭圆;
=1(a≠b)表示焦点在x轴上的椭圆;
④已知抛物线y2=2px(p>0)的焦点弦AB的两端点坐标分别为A(x1 , y2),B(x2 , y2),则 ![]() =﹣4
=﹣4
其中的真命题是 . (把你认为是真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为![]() 的椭圆
的椭圆![]() 的一个焦点为圆
的一个焦点为圆![]() :
: ![]() 的圆心.
的圆心.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,过
上一点,过![]() 作两条斜率之积为
作两条斜率之积为![]() 的直线
的直线![]() ,
, ![]() ,当直线
,当直线![]() ,
, ![]() 都与圆
都与圆![]() 相切时,求
相切时,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图. 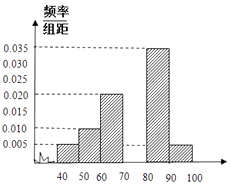
(1)求抽出的60名学生中分数在[70,80)内的人数;
(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校优秀人数.
(3)根据频率分布直方图算出样本数据的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:对任意的x1 , x2∈R(x1≠x2),有 ![]() <0,则( )
<0,则( )
A.f(3)<f(﹣2)<f(1)
B.f(1)<f(﹣2)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(1)<f(﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com