
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 对于①②③新定义函数类型的题目,解答时要先充分理解定义:“平缓函数”才能答题,对于(1)只需按照定义作差:|f(x1)-f(x2)|,然后寻求|f(x2)-f(x1)|≤|x2-x1|成立的条件.
对于④的解答稍微复杂一些,此处除了用到放缩外,还有添项减项的技巧应用及对数列拆项求和的充分利用.
解答 解:对于①,|f(x1)-f(x2)|=|-lnx1+x1-(-lnx2+x2)|=|ln$\frac{{x}_{2}}{{x}_{1}}$+x1-x2|≤|ln$\frac{{x}_{2}}{{x}_{1}}$|+|x1-x2|,故均有|f(x1)-f(x2)|<|x1-x2|不一定成立,
故f(x)=-lnx+x不为(0,+∞)上的“平缓函数”,故①错误;
对于②,设φ(x)=x-sinx,则φ'(x)=1-cosx≥0,则φ(x)=x-sinx是实数集R上的增函数,
不妨设x1<x2,则φ(x1)<φ(x2),即x1-sinx1<x2-sinx2,
则sinx2-sinx1<x2-x1,①
又y=x+sinx也是R上的增函数,则x1+sinx1<x2+sinx2,
即sinx2-sinx1>x1-x2,②
由①、②得-(x2-x1)<sinx2-sinx1<x2-x1,
因此|sinx2-sinx1|<|x2-x1|,对x1<x2的实数都成立,
当x1>x2时,同理有|sinx2-sinx1|<|x2-x1|成立,
又当x1=x2时,不等式|sinx2-sinx1|=|x2-x1|=0,
故对任意的实数x1,x2∈R均 有|sinx2-sinx1|≤|x2-x1|,
因此sinx是R上的“平缓函数,故②正确;
对于③,取x1=3,x2=1,则|h(x1)-h(x2)|=4>|x1-x2|,因此h(x)=x2-x不是R上的“平缓函数”,故③错误,
对于④,函数y=k(x)为R上的“平缓函数,
则|k(x2)-k(x1)|≤|x2-x1|,所以|yn+1-yn|≤|xn+1-xn|,
因为|xn+1-xn|≤$\frac{1}{{(2n+1)}^{2}}$<$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),
而|yn+1-y1|=|(yn+1-yn)+(yn-yn-1)+(yn-1-yn-2)+…(y2-y1)|,
所以|yn+1-y1|≤|yn+1-yn|+|yn-1-yn-2|+…+|y2-y1|,
∴|yn+1-y1|≤$\frac{1}{4}$[($\frac{1}{n}$-$\frac{1}{n+1}$)+($\frac{1}{n-1}$-$\frac{1}{n}$)+…+(1-$\frac{1}{2}$)]=$\frac{1}{4}$(1-$\frac{1}{n+1}$)<$\frac{1}{4}$,故④正确.
故选:C.
点评 本题抽象函数、新定义函数类型的概念,不等式的性质,放缩法的技巧,对于新定义类型问题,在解答时要先充分理解定义才能答题,避免盲目下笔,遇到困难才来重头读题,费时费力,另外要在充分抓住定义的基础上,对式子的处理要灵活,各个式子的内在联系要充分挖掘出来,可现有结论向上追溯,看看需要哪些条件才能得出结果,再来寻求转化取得这些条件.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | k<-4 | B. | -4<k<0> | C. | -2<k<0 | D. | k>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
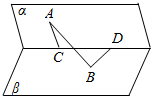 如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求:
如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com