
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/ | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
热饮杯数 | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是![]() ,预测这天卖出的热饮杯数.
,预测这天卖出的热饮杯数.
【答案】(1)解析见散点图;(2)气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少;(3)![]()
![]() ;(4)
;(4)![]() .
.
【解析】试题分析:(1)根据数据,画出散点图;(2)观察得到气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少;(3)利用回归方程的公式求出回归系数![]() ,
,![]() ,得到回归方程;(4)当x=2时,
,得到回归方程;(4)当x=2时, ![]() =143.063.因此,某天的气温为2 ℃时,这天大约可以卖出143杯热饮.
=143.063.因此,某天的气温为2 ℃时,这天大约可以卖出143杯热饮.
试题解析:
(1)散点图如图所示:
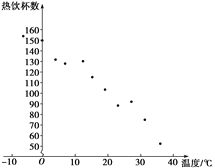
(2)从上图看到,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少.
(3)从散点图可以看出,这些点大致分布在一条直线的附近,因此,可用公式求出回归方程的系数.利用计算器容易求得回归方程![]() =-2.352x+147.767.
=-2.352x+147.767.
(4)当x=2时, ![]() =143.063.因此,某天的气温为2 ℃时,这天大约可以卖出143杯热饮.
=143.063.因此,某天的气温为2 ℃时,这天大约可以卖出143杯热饮.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】直线l经过两直线l1:2x-y+4=0与l2:x-y+5=0的交点,且与直线x-2y-6=0垂直.
(1)求直线l的方程.
(2)若点P(a,1)到直线l的距离为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较.在试制某种牙膏新品种时,需要选用两种不同的添加剂.现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用.根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验.(写解题过程)
(1)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(2)求所选用的两种不同的添加剂的芳香度之和不小于3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点的零件的多少随机器的运转的速度的变化而变化,下表为抽样试验的结果:
转速 | 16 | 14 | 12 | 8 |
每小时生产有缺点的零件数 | 11 | 9 | 8 | 5 |
(1)画出散点图;
(2)如果![]() 对
对![]() 有线性相关关系,请画出一条直线近似地表示这种线性关系;
有线性相关关系,请画出一条直线近似地表示这种线性关系;
(3)在实际生产中,若它们的近似方程为![]() ,允许每小时生产的产品中有缺点的零件最多为
,允许每小时生产的产品中有缺点的零件最多为![]() 件,那么机器的运转速度应控制在什么范围内?
件,那么机器的运转速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .直线
.直线![]() 过点
过点![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,求|a+b|和a+b与c的夹角;
(2)设O为△ABC的外心,已知AB=3,AC=4,非零实数x,y满足![]() =x
=x![]() +y
+y![]() ,且x+2y=1,求cos ∠BAC的值.
,且x+2y=1,求cos ∠BAC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com