
 如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y.
如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y.分析 (1)作OH,DN分别垂直DC,AB交于H,N,连结OD,求出OH,又在直角△AND中,进一步求出AD,从而求出梯形ABCD的周长y与x间的函数解析式,根据AD>0,AN>0,CD>0可求出定义域;
(2)利用二次函数在给定区间上求出最值的知识可求出函数的最大值.
解答 解:(1)作OH,DN分别垂直DC,AB交于H,N,
连结OD.由圆的性质,H是中点,设OH=h,
h=$\sqrt{O{D}^{2}-D{H}^{2}}=\sqrt{4-{x}^{2}}$.
又在直角△AND中,AD=$\sqrt{A{N}^{2}+D{N}^{2}}=\sqrt{(2-x)^{2}+(4-{x}^{2})}$=$\sqrt{8-4x}$=2$\sqrt{2-x}$,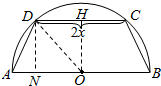
∴y=f(x)=AB+2AD+DC=4+2x+4$\sqrt{2-x}$,其定义域是(0,2);
(2)令t=$\sqrt{2-x}$,则t∈(0,$\sqrt{2}$),且x=2-t2,
∴y=4+2•(2-t2)+4t=-2(t-1)2+10,
当t=1,即x=1时,y的最大值是10.
点评 本题考查了函数的最值及其几何意义,考查了二次函数在解决实际问题中求解最值的常用的方法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com