
����Ŀ����֪��Բ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ���ҵ�
���ҵ�![]() ����ԲC��.
����ԲC��.
��1������ԲC�ı����̣�
��2������Բ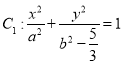 �������䶥�������һ��Q��Բ
�������䶥�������һ��Q��Բ![]() ���������ߣ��е�ֱ�Ϊ
���������ߣ��е�ֱ�Ϊ![]() �����������ϣ�����ֱ��
�����������ϣ�����ֱ��![]() ��x�ᣬy���ϵĽؾ�ֱ�Ϊ
��x�ᣬy���ϵĽؾ�ֱ�Ϊ![]() ��֤����
��֤����![]() Ϊ��ֵ��
Ϊ��ֵ��
��3����![]() ����Բ
����Բ![]() �ϲ�ͬ���㣬
�ϲ�ͬ���㣬![]() �ᣬԲE��
�ᣬԲE��![]() ������Բ
������Բ![]() ������һ�㶼����ԲE�ڣ����ԲEΪ����Բ��һ������Բ�����ʣ���Բ
������һ�㶼����ԲE�ڣ����ԲEΪ����Բ��һ������Բ�����ʣ���Բ![]() �Ƿ���ڹ�����F������Բ�������ڣ����Բ��E�����ꣻ�������ڣ���˵�����ɣ�
�Ƿ���ڹ�����F������Բ�������ڣ����Բ��E�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��֤������������3��
����2��֤������������3��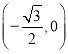 .
.
��������
��1���ɽ�������ȷ����c��ֵ��������Բ�������г�a��b�ķ��̣��ٽ�P�����������Բ�����г�����a��b�ķ��̣��������a��b��ֵ��ȷ������Բ���̼��ɣ�
��2�������⣺ȷ����C1�ķ��̣����P��x1��y1����M��x2��y2����N��x3��y3��������M��N�����������ϣ��õ�ֱ��PM��ֱ��OMб�ʳ˻�Ϊ��1��ȷ����ֱ��PM�ķ��̣�ͬ���ɵ�ֱ��PN�ķ��̣�����ȷ����ֱ��MN���̣����ֱ��MN��x�ᣬy��ؾ�m��n������ȷ��������ʽ�ӵ�ֵΪ��ֵ��
��3��������ɵ÷���Ҫ���ԲE����Ϊ����F��P1��P2�������ε����Բ������Բ����x���ϣ���������д��ԲE�ķ��̣�����Բ�Ĵ��ڱ���Ҫ���ϣ���Բ�ϵĵ㵽ԲE�������Сֵ��|P1E|�����ͼ�οɵ�Բ��E���߶�P1P2�ϣ��뾶��С�������ڵ�F��֪��������ý��ۣ�
��1������ԲC��![]() ���ҽ���ΪF��1��0�����ҵ�P��1,
���ҽ���ΪF��1��0�����ҵ�P��1,![]() ������ԲC�ϣ�
������ԲC�ϣ�
��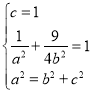 �����a��2��b��
�����a��2��b��![]() ��
��
����ԲC�ı�����Ϊ![]() ��
��
��2�������⣺C1��![]() ��
��
���P��x1��y1����M��x2��y2����N��x3��y3����
��M��N�����������ϣ���kPM����![]() ����
����![]() ��
��
��ֱ��PM�ķ���Ϊy��y2����![]() ��x��x2����
��x��x2����
����ã�x2x+y2y��![]() ���٣�
���٣�
ͬ���ɵ�ֱ��PN�ķ���Ϊx3x+y3y��![]() ���ڣ�
���ڣ�
��P����������١��ڵ�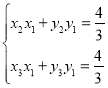 ��
��
��ֱ��MN�ķ���Ϊx1x+y1y��![]() ��
��
��y��0����m��![]() ����x��0��n��
����x��0��n��![]() ��
��
��x1��![]() ��y1��
��y1��![]() ��
��
�ֵ�P����ԲC1�ϣ�
�ࣨ![]() ��2+3��
��2+3��![]() ��2��4��
��2��4��
��![]() ��
��![]() Ϊ��ֵ��
Ϊ��ֵ��
��3������Բ�ĶԳ��ԣ�������P1��m��n����P2��m����n������E��x���ϣ����E��t��0����
��ԲE�ķ���Ϊ����x��t��2+y2����m��t��2+n2��
������Բ����֪������Բ�ϵĵ㵽��E�������Сֵ��|P1E|��
���M��x��y������ԲC������һ�㣬��|ME|2����x��t��2+y2��![]() ��
��
��x��mʱ��|ME|2��С����m����![]() ���ۣ�
���ۣ�
��ԲE����F���ࣨ��![]() ��2����m��t��2+n2����
��2����m��t��2+n2����
��P1����Բ�ϣ���![]() ����
����
�ɢۢܢݣ���ã�t����![]() ��t����
��t����![]() ��
��
��t����![]() ʱ��m����
ʱ��m����![]() ����2���������⣬
����2���������⣬
���ϣ���ԲC���ڷ�������������Բ����E�������ǣ���![]() ��0����
��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)=lg ![]() ��f(1)=0����x>0ʱ������f(x)
��f(1)=0����x>0ʱ������f(x)![]() =lgx.
=lgx.
(1)������ʽf(x)��lgt�Ľ⼯ΪA����A(0,4]����ʵ��t��ȡֵ��Χ��
(2)������f(x)=lg(8x+m)�Ľ⼯Ϊ����ʵ��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �������
�������![]() ����:
����:![]() ,��
,��![]() ʱ,
ʱ,![]()
��1�����������R����㣻
��2�������㲻��ʽ![]() ��ʵ��
��ʵ��![]() �ķ�Χ.
�ķ�Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() .
.
��1�����ۺ���![]() �ļ�ֵ��ĸ�����
�ļ�ֵ��ĸ�����
��2����![]() ��������ֵ��
��������ֵ��![]()
![]() ��֤����
��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ļ����ºͶ�����ůʱ������Դ��ģ����ݵ��ݶ�����ǽ��Ҫ������Ȳ㡣ij��������Ҫ�����ʹ��20��ĸ��Ȳ㣬ÿ����ĸ��Ȳ㽨��ɱ�Ϊ6��Ԫ���ý�����ÿ�����Դ���ķ���C����λ����Ԫ������Ȳ���x����λ��cm�������ϵ��C��x��=![]() ���������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�͡�
���������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�͡�
��������k��ֵ��f(x)�ı���ʽ��
���������Ȳ������ʱ���ܷ���f(x)�ﵽ��С��������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��11��18�չ�����������ǹ���籭�ܾ������������ۺ������ݿ�Ļ�����ǹ�����������ǹ���籭�ܾ���ʱ��10���ٶ��߽��й�.Ϊ����ǿȤζ�ԣ���ʵʱ�����ֳ���������У�ֳ�С���������Ͳ���С�������������һ�ײ���ת�뷨�����ͷ������������ģ����ܣ������ܷ������������ģ����ܣ�����֪���ܵķ����ǣ������Ӣ�ĵ����ģ���ʵ�ģ�����ĸ�ֽ⣬����Ӣ�ĵ�![]() ��26����ĸ�����۴�Сд�����ζ�Ӧ1��2��3������26��26����Ȼ��ͨ���任��ʽ��
��26����ĸ�����۴�Сд�����ζ�Ӧ1��2��3������26��26����Ȼ��ͨ���任��ʽ�� ��������ת�������ģ���
��������ת�������ģ���![]() ����
����![]() �任��
�任��![]() ����
����![]() �任��
�任��![]() .���������涨���������յ���������
.���������涨���������յ���������![]() ����ôԭ���������ǣ� ��
����ôԭ���������ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ��������Ϊ
��������Ϊ![]() ����AΪ����Բ���㣬���ҽ���
����AΪ����Բ���㣬���ҽ���![]() ��ֱ��l����Բ����B��C���㣬��
��ֱ��l����Բ����B��C���㣬��![]() ��ʱ��������ABC�����Ϊ18��
��ʱ��������ABC�����Ϊ18��
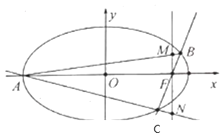
![]() ����Բ
����Բ![]() �ķ��̣�
�ķ��̣�
![]() ��ͼ������ֱ��BCб�ʴ����Ҳ�Ϊ0ʱ��ֱ��
��ͼ������ֱ��BCб�ʴ����Ҳ�Ϊ0ʱ��ֱ��![]() �ֱ�ֱ��AB��AC�ڵ�M��N����x�����Ƿ���ڵ�P��ʹ��
�ֱ�ֱ��AB��AC�ڵ�M��N����x�����Ƿ���ڵ�P��ʹ��![]() �������������P�����ꣻ��������˵�����ɣ�
�������������P�����ꣻ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���������·ݣ��ҹ����������ε����������25�����ҵ�÷�꼾�ڣ���ͼ�ǽ���ij����![]() ��10���÷�꼾�ڵĽ�����
��10���÷�꼾�ڵĽ�����![]() ��λ��
��λ��![]() ��Ƶ�ʷֲ�ֱ��ͼ����������Ƶ�ʹ���������ʣ�����������⣺
��Ƶ�ʷֲ�ֱ��ͼ����������Ƶ�ʹ���������ʣ�����������⣺
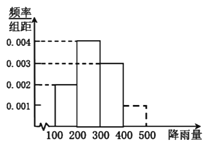
![]() ����ÿ���÷�꼾���������������õ���δ������������������÷�꼾�ڵĽ���������350mm�ĸ��ʣ�
����ÿ���÷�꼾���������������õ���δ������������������÷�꼾�ڵĽ���������350mm�ĸ��ʣ�
![]() �����ڸõ����а���20Ķ������ֲ��÷������ȥ��ֲ�ļ�Ʒ����÷��ƽ��ÿ���������Ϊ28��Ԫ
�����ڸõ����а���20Ķ������ֲ��÷������ȥ��ֲ�ļ�Ʒ����÷��ƽ��ÿ���������Ϊ28��Ԫ![]() ����Ʒ����÷��Ķ����
����Ʒ����÷��Ķ����![]() Ķ
Ķ![]() �뽵����֮��Ĺ�ϵ������ͳ�Ʊ���ʾ����֪��Ʒ����÷�ĵ�λ����Ϊ
�뽵����֮��Ĺ�ϵ������ͳ�Ʊ���ʾ����֪��Ʒ����÷�ĵ�λ����Ϊ![]() Ԫ
Ԫ![]() ������������������������Ӧ����ֲ�ĸ�Ʒ�ֵ���÷����ʹ������
������������������������Ӧ����ֲ�ĸ�Ʒ�ֵ���÷����ʹ������![]() ��Ԫ
��Ԫ![]() ����������˵�����ɣ�
����������˵�����ɣ�
������ |
|
|
|
|
Ķ���� | 500 | 700 | 600 | 400 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɹ���һ��ͨ���������㹺�����ʽ��ij���ͳ���Ϊ����˿����ɹ���ʹ������������ȡ��100�ˣ��������������£�
20���� | [20��30�� | [30��40�� | [40��50�� | [50��60�� | [60��70] | 70���� | |
ʹ������ | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
δʹ������ | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
��1���������ȡ1���˿ͣ��Թ��Ƹù˿�������[30��50����δʹ�����ɹ��ĸ��ʣ�
��2���ӱ���ȡ��������[50��70]ʹ�õ����ɹ��˿��У������ȡ2�˽�һ���˽����������2�����䶼��[50��60���ĸ��ʣ�
��3��Ϊ�����˿�ʹ�����ɹ����ó������ʹ�����ɹ��˿�����1���������������ij�ոó���Ԥ����5000�˹���Թ��Ƹó��е�������Ӧ�����ٸ������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com