
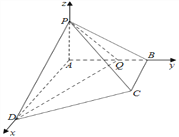
【题目】四棱锥![]() 中,
中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,BC//AD,已知Q是四边形ABCD内部一点,且二面角
,BC//AD,已知Q是四边形ABCD内部一点,且二面角![]() 的平面角大小为
的平面角大小为![]() ,若动点Q的轨迹将ABCD分成面积为
,若动点Q的轨迹将ABCD分成面积为![]() 的两部分,则
的两部分,则![]() =_______.
=_______.
【答案】![]()
【解析】以A为坐标原点建立空间直角坐标系,如图:设Q的轨迹与y轴的交点坐标为Q(0,b,0)(b>0).
由题意可知A(0,0,0),D(2,0,0),P(0,0,1),
∴![]() =(﹣2,0,1),
=(﹣2,0,1),![]() =(﹣2,b,0).
=(﹣2,b,0). ![]() =(2,0,0).
=(2,0,0).
设平面APD的法向量为![]() =(x1,y1,z1),平面PDQ的法向量为
=(x1,y1,z1),平面PDQ的法向量为![]() =(x2,y2,z2)
=(x2,y2,z2)
则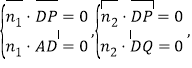
即![]() ,
,
令y1=0得![]() =(0,1,0),令z2=2得
=(0,1,0),令z2=2得![]() =(1,
=(1,![]() ,2).
,2).
∴![]() .
.
∵二面角Q﹣PD﹣A的平面角大小为![]() ,
,
∴cos<![]() >=
>= 即
即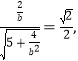 解得b=
解得b=![]() .
.
∴S△ADQ=![]() .
.
S梯形ABCD﹣S△ADQ=![]() .
.
∵S1<S2,∴S1=![]() ,S2=
,S2=![]() .∴S1:S2=(3
.∴S1:S2=(3![]() ﹣4):4.
﹣4):4.
故答案为(3![]() ﹣4):4.
﹣4):4.


科目:高中数学 来源: 题型:
【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查,其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下:
地铁站 | 世界之窗 | 白石州 | 高新园 | 深大 | 桃园 | 大新 |
满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
已知6个站的平均得分为75分.
(1)求大新站的满意度得分x,及这6个站满意度得分的标准差;
(2)从表中前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是:
的参数方程是: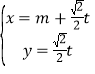 (
(![]() 是参数,
是参数,![]() 是常数).以
是常数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
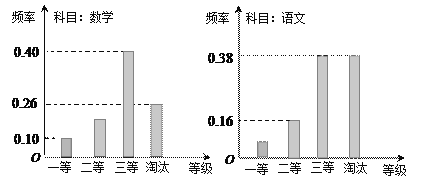

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产品经销商销售某种鲜鱼,售价为每公斤![]() 元,成本为每公斤
元,成本为每公斤![]() 元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失
元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失![]() 元.根据以往的销售情况,按
元.根据以往的销售情况,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到如图所示的频率分布直方图.
进行分组,得到如图所示的频率分布直方图.
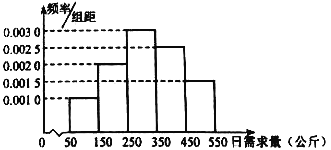
(1)求未来连续三天内,该经销商有连续两天该种鲜鱼的日销售量不低于![]() 公斤,而另一天日销售量低于
公斤,而另一天日销售量低于![]() 公斤的概率;
公斤的概率;
(2)在频率分布直方图的需求量分组中,以各组区间的中点值代表该组的各个值.
(i)求日需求量![]() 的分布列;
的分布列;
(ii)该经销商计划每日进货![]() 公斤或
公斤或![]() 公斤,以每日利润
公斤,以每日利润![]() 的数学期望值为决策依据,他应该选择每日进货
的数学期望值为决策依据,他应该选择每日进货![]() 公斤还是
公斤还是![]() 公斤?
公斤?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆与圆![]() 相切,且与圆
相切,且与圆![]() 相内切,记圆心的轨迹为曲线.
相内切,记圆心的轨迹为曲线.
(Ⅰ)求曲线C的方程;
(Ⅱ)设Q为曲线C上的一个不在轴上的动点,O为坐标原点,过点![]() 作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
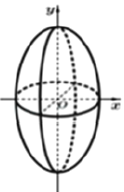
【题目】祖暅是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原理:“幂势既同,则积不容易.”这里的“幂”指水平截面的面积.“势”指高,这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。于是可把半径相等的半球(底面在下)和圆柱(圆柱高等于半径)放在同一水平面上,圆柱里再放一个半径和高都与圆柱相等的圆锥(锥尖朝下),考察圆柱里被圆锥截剩的立体,这样在同一高度用平行平面截得的半球截面和圆柱中剩余立体截得的截面面积相等,因此半球的体积等于圆柱中剩余立体的体积.设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种产品的质量,从中分别随机抽取了10件样品,测量产品中某种元素的含量(单位:毫克),如图所示是测量数据的茎叶图.规定:当产品中的此中元素的含量不小于18毫克时,该产品为优等品.

(1)试用样品数据估计甲、乙两种产品的优等品率;
(2)若从甲、乙两种产品的优等品中各随机抽取1件,抽到的2件优等品中,“甲产品的含量28毫克优等品必须在内,且乙产品的含量28毫克优等品不包含在内”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com