
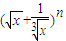 的展开式的各项系数和为64,则展开式中系数最大的项是 .
的展开式的各项系数和为64,则展开式中系数最大的项是 . 科目:高中数学 来源:四川省成都外国语学院高三2010-2011学年9月月考数学试题(理科) 题型:填空题
有以下命题:①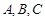 是表面积为
是表面积为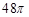 的球面
的球面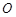 (
(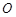 为球心)上的三点,若
为球心)上的三点,若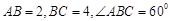 ,则三棱锥
,则三棱锥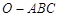 的体积为
的体积为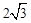 ;②二项式
;②二项式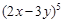 的展开式的各项的系数和为
的展开式的各项的系数和为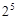 ;③已知函数
;③已知函数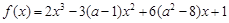 在
在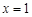 处取得极值,则实数
处取得极值,则实数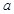 的值是
的值是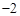 或
或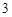 ;④已知点
;④已知点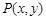 是抛物线
是抛物线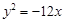 的准线与双曲线
的准线与双曲线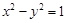 的两条渐近线所围成的三角形区域(含边界)内的任意一点,则
的两条渐近线所围成的三角形区域(含边界)内的任意一点,则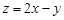 的最大值为9。其中正确命题的序号有__________
的最大值为9。其中正确命题的序号有__________
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州市江陵实验高中高二(上)综合测试数学试卷(解析版) 题型:选择题
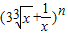 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省宁波市鄞州高级中学高二(上)期末数学试卷(理科)(解析版) 题型:选择题
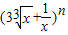 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第84课时):第十章 排列、组合和概率-二项式定理(1)(解析版) 题型:选择题
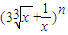 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n=( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com