
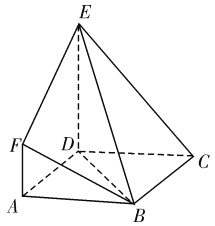
【题目】如图,![]() 是边长为3的正方形,
是边长为3的正方形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(1)试在线段![]() 上确定一点
上确定一点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
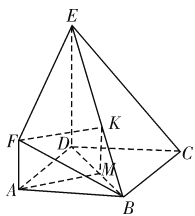
【解析】分析:(1)设平面ACF与BD交于点M,与BE交于点N,M点就量所求,由此可知M是BD的三等分点中靠近B点的一个,由线面平行的判定定理可证;
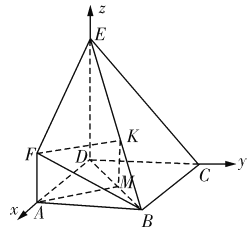
(2)分别以DA,DC,DE为![]() 轴建立空间直角坐标系,写出各点坐标,求出平面ABE和平面CBE的法向量,由法向量的夹角可得所求二面角.
轴建立空间直角坐标系,写出各点坐标,求出平面ABE和平面CBE的法向量,由法向量的夹角可得所求二面角.
详解:(1)证明:取![]() 的三等分点
的三等分点![]() (靠近点
(靠近点![]() ),过
),过![]() 作
作![]() 交
交![]() 于
于![]() ,则有
,则有![]() ,由
,由![]() 平面
平面![]() ,
,![]() ,可知
,可知![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() ,且
,且![]() .
.
∴四边形![]() 为平行四边形,可知
为平行四边形,可知![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]() 为
为![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ).
).
(2)如图建立空间直角坐标系:则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 可得
可得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 可得
可得![]() ,
,
因为二面角![]() 为钝二面角,可得
为钝二面角,可得![]() ,
,
所以二面角![]() 余弦值为
余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x),g(x)分别由下表给出,


则f[g(1)]的值为________,满足f[g(x)]>g[f(x)]的x的值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如图:
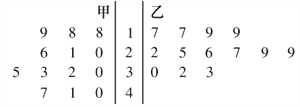
根据上图,对这两名运动员地成绩进行比较,下列四个结论中,不正确的是
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员的得分平均值大于乙运动员的得分平均值
D. 甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:

(1)现要在这10户家庭中任意选取3家,求取到第二阶梯水量的户数![]() 的分布列与数学期望;
的分布列与数学期望;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为二阶的可能性最大,求
户月用水量为二阶的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 作不与
作不与![]() 轴重合的直线
轴重合的直线![]() ,设
,设![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与椭圆相交于
两点,与椭圆相交于![]() 两点,当
两点,当![]() 且
且![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面
B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行
C.平行于同一条直线的两个平面平行
D.若直线a,b和平面α满足a∥b,a∥α,b不在平面α内,则b∥α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 和
和![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的面积为
的面积为![]() .
.
(1)求该椭圆的标准方程;
(2)过该椭圆的左顶点![]() 作两条相互垂直的直线分别与椭圆相交于不同于点
作两条相互垂直的直线分别与椭圆相交于不同于点![]() 的两点
的两点![]() 、
、![]() ,证明:动直线
,证明:动直线![]() 恒过
恒过![]() 轴上一定点.
轴上一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com