Question

3．已知直线l：x-$\sqrt{3}$y+3=0与椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1交于A，B两点，过A，B分别作l的垂线与x轴交于C，D两点，则|CD|=（　　）

• A． $\sqrt{3}$
• B． $\frac{16}{13}$
• C． $\frac{32}{13}$
• D． $\frac{30}{13}$

Answer 1

分析 联立$\left\{\begin{array}{l}{x-\sqrt{3}y+3=0}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$，得13y²-18$\sqrt{3}y$+15=0，利用弦长公式出|AB|，直线l：x-$\sqrt{3}$y+3=0的倾斜角为30°，从而|CD|=$\frac{|AB|}{cos30°}$，由此能求出结果．

解答 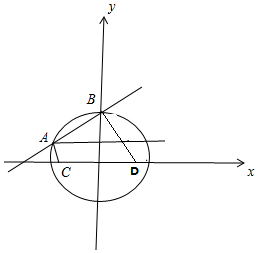解：联立$\left\{\begin{array}{l}{x-\sqrt{3}y+3=0}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$，
得13y²-18$\sqrt{3}y$+15=0，
设A（x₁，y₁），B（x₂，y₂），则y₁+y₂=$\frac{18\sqrt{3}}{13}$，
y₁y₂=$\frac{15}{13}$，
|AB|=$\sqrt{4[（\frac{18\sqrt{3}}{13}）^{2}-4×\frac{15}{13}]}$=$\frac{16\sqrt{3}}{13}$，
∵直线l：x-$\sqrt{3}$y+3=0的倾斜角为30°，
∴|CD|=$\frac{|AB|}{cos30°}$=$\frac{\frac{16\sqrt{3}}{13}}{\frac{\sqrt{3}}{2}}$=$\frac{32}{13}$．
故选：C．

点评 本题考查线段长的求法，是中档题，解题时要认真审题，注意根的判别式、韦达定理、弦长公式、椭圆性质的合理运用．