
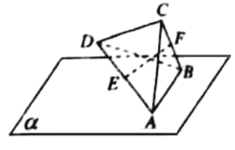
【题目】在四面体![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,现将四面体以
的中点,现将四面体以![]() 为轴旋转,则线段
为轴旋转,则线段![]() 在平面内投影长度的取值范围是__________.
在平面内投影长度的取值范围是__________.
【答案】![]()
【解析】
取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,利用三角形的中位线得
,利用三角形的中位线得![]() ,
,![]() ,根据等腰三角形的性质和线面垂直的判定定理,可证出
,根据等腰三角形的性质和线面垂直的判定定理,可证出![]() 平面
平面![]() ,进而得出
,进而得出![]() ,
,![]() ,当四面体绕
,当四面体绕![]() 旋转时,
旋转时,![]() 与
与![]() 的垂直性保持不变,当
的垂直性保持不变,当![]() 与平面
与平面![]() 垂直时,
垂直时,![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最小值,当
的长取得最小值,当![]() 与平面
与平面![]() 平行时,
平行时,![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最大值,由此即可得出结果.
的长取得最大值,由此即可得出结果.
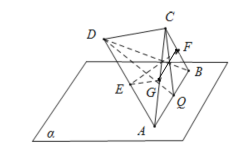
解:如图,取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() 分别是线段
分别是线段![]() 和
和![]() 的中点,
的中点,
![]() ,
,![]() ,
,
由于![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
当四面体绕![]() 旋转时,
旋转时,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 与
与![]() 的垂直性保持不变,且
的垂直性保持不变,且![]() ,长度不变,
,长度不变,
当![]() 与平面
与平面![]() 垂直时,
垂直时,![]() 在平面上的射影长最短为0,
在平面上的射影长最短为0,
此时![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最小值为
的长取得最小值为![]() ,
,
当![]() 与平面
与平面![]() 平行时,
平行时,![]() 在平面上的射影长最长为:
在平面上的射影长最长为:![]() ,
,
此时![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最大值为
的长取得最大值为![]() ,
,
![]() 线段
线段![]() 在平面
在平面![]() 上的射影长的取值范围是
上的射影长的取值范围是![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】某企业接到生产3000台某产品的![]() 三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产![]() 部件的人数为
部件的人数为![]() ,分别写出完成
,分别写出完成![]() 三种部件生产需要的时间;
三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数之和不少于![]() 次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为
次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为![]() .
.
(1)若![]() ,
,![]() ,则在第一轮游戏他们获“优秀小组”的概率;
,则在第一轮游戏他们获“优秀小组”的概率;
(2)若![]() 则游戏中小明小亮小组要想获得“优秀小组”次数为
则游戏中小明小亮小组要想获得“优秀小组”次数为![]() 次,则理论上至少要进行多少轮游戏才行?并求此时
次,则理论上至少要进行多少轮游戏才行?并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会经济高速发展,人民的生活水平越来越高,部分学校安装了中央空调,某校数学建模队调查了某品牌中央空调,得到该设备使用年限x(单位:年)和维修总费用y(单位:万元)的统计表如下:(每年年底维修保养)
使用年限x(单位:年) | 2 | 3 | 4 | 5 | 6 |
维修总费用y(单位:万元) | 1 |
| 3 | 4 |
|
由上表可得线性回归方程![]() ,则根据此模型预报该品牌中央空调第8年年底的维修费用约为( )
,则根据此模型预报该品牌中央空调第8年年底的维修费用约为( )
A.![]() 万元B.
万元B.![]() 万元C.
万元C.![]() 万元D.
万元D.![]() 万元
万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com