
| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
分析 根据$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=2$\overrightarrow{AB}$,可得3$\overrightarrow{AP}$=$\overrightarrow{BC}$,所以$\overrightarrow{AP}$∥$\overrightarrow{BC}$并且方向一样,由此可求S△PAB.
解答  解:∵$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=2$\overrightarrow{AB}$=2($\overrightarrow{AP}$+$\overrightarrow{PB}$)
解:∵$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=2$\overrightarrow{AB}$=2($\overrightarrow{AP}$+$\overrightarrow{PB}$)
∴3$\overrightarrow{AP}$=$\overrightarrow{BC}$
∴$\overrightarrow{AP}$∥$\overrightarrow{BC}$并且方向一样
设AP与BC的距离为h,则
∵S△PAB=$\frac{1}{2}$|$\overrightarrow{AP}$|h,S△ABC=$\frac{1}{2}$|$\overrightarrow{BC}$|h
∵|$\overrightarrow{BC}$|=3|$\overrightarrow{AP}$|,S△ABC=12
∴S△PAB=$\frac{1}{3}$S△ABC=4
故选A.
点评 本题考查向量知识的运用,考查三角形面积的计算,解题的关键是确定$\overrightarrow{AP}$∥$\overrightarrow{BC}$并且方向一样.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 评分 | 1 | 2 | 3 | 4 | 5 |
| 人数 | x | 20 | 10 | 5 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
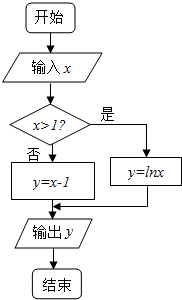 某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.
某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [-2,2) | C. | [-3,2] | D. | [-3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com