[题目]在平面直角坐标系中.O为坐标原点.以O为圆心的圆与直线相切．(1)求圆O的方程．(2)直线与圆O交于A.B两点.在圆O上是否存在一点M.使得四边形为菱形?若存在.求出此时直线l的斜率,若不存在.说明理由．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在平面直角坐标系中，O为坐标原点，以O为圆心的圆与直线相切．

(1)求圆O的方程．

(2)直线与圆O交于A，B两点，在圆O上是否存在一点M，使得四边形为菱形？若存在，求出此时直线l的斜率；若不存在，说明理由．

【答案】（1）x2+y2=4.（2）直线l的斜率为±2.

【解析】

试题（1）先根据圆心到切线距离等于半径求，再根据标准式写圆方程（2）由题意得OM与AB互相垂直且平分,即得原点O到直线l的距离，再根据点到直线距离公式求直线斜率

试题解析：（1）设圆O的半径长为r,因为直线x-y-4=0与圆O相切,所以 r=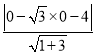=2.

所以圆O的方程为 x2+y2=4.

（2）假设存在点M,使得四边形OAMB为菱形,则OM与AB互相垂直且平分,

所以原点O到直线l:y=kx+3的距离d=|OM|=1.所以=1,解得k2=8,即k=±2,经验证满足条件.所以存在点M,使得四边形OAMB为菱形，此时直线l的斜率为±2.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】等比数列{an}的各项均为正数，且2a1＋3a2＝1，＝9a2a6.

(1)求数列{an}的通项公式；

(2)设bn＝log3a1＋log3a2＋…＋log3an，求数列的前n项和．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，E为BD的中点，G为PD的中点，△DAB≌△DCB，EA=EB=AB=1，PA= ，连接CE并延长交AD于F

（1）求证：AD⊥平面CFG；
（2）求平面BCP与平面DCP的夹角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司生产一种产品，每年投入固定成本万元.此外，每生产件这种产品还需要增加投入万元.经测算，市场对该产品的年需求量为件，且当出售的这种产品的数量为（单位：百件）时，销售所得的收入约为（万元）.

（1）若该公司这种产品的年产量为（单位：百件），试把该公司生产并销售这种产品所得的年利润表示为年产量的函数；

（2）当该公司的年产量为多少时，当年所得利润最大？最大为多少？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知点(0,1),(3+2,0),(3-2,0)在圆C上.

(1)求圆C的方程.

(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知等差数列{an}的公差不为零，a1＝25，且a1，a11，a13成等比数列．

(1)求{an}的通项公式；

(2) 是{an}的前n项和，求的最大值。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以x（单位：t，100≤x≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．

（1）将T表示为x的函数；
（2）根据直方图估计利润T不少于57000元的概率；
（3）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中点值的概率（例如：若x∈[100，110））则取x=105，且x=105的概率等于需求量落入[100，110）的频率，求T的数学期望．