
���� ��1�����P�����꣬���OP��OQ��PQ��б�ʣ�����$\frac{1}{{{k_{OP}}}}+\frac{1}{{{k_{OQ}}}}=\frac{1}{{{k_{PQ}}}}$�������ɵõ�P�Ĺ켣C�ķ��̣�
��2����F����б��Ϊ60���ֱ��L��������C����������Τ�ﶨ�����������AOB�������
��3����ֱ��l1�ķ���Ϊy=k��x-1����k��0�����������߷�����������Ϊ����x��һԪ���η��̣����ø���ϵ���Ĺ�ϵ���E�����꣬ͬ�����F�����꣬��һ�����EF����ֱ�߷��̣�����ϵ����֤��ֱ��EF���һ���㣮
��� �⣺��1�����P������ΪP��x��y������2�֣�
��$\frac{1}{{{k_{OP}}}}+\frac{1}{{{k_{OQ}}}}=\frac{1}{{{k_{PQ}}}}$����$\frac{x}{y}+\frac{1}{2}=\frac{x-1}{y-2}$��
�����õ�P�Ĺ켣�ķ���Ϊ��y2=4x��y��0��y��2���� ����4�֣�
��2����A��x1��y1����B��x2��y2������$\left\{\begin{array}{l}{y^2}=4x\\ y=\sqrt{3}��x-1��\end{array}\right.$
�ã�${y^2}-\frac{4}{3}\sqrt{3}y-4=0$��
��${y_1}+{y_2}=\frac{4}{3}\sqrt{3}\;\;��\;\;{y_1}{y_2}=-4$����6�֣�
��${S_��}=\frac{1}{2}��|OF|��|{y_2}-{y_1}|$=$\frac{1}{2}��1��\sqrt{{{��{y_1}+{y_2}��}^2}-4{y_1}{y_2}}$=$\frac{1}{2}•\sqrt{\frac{16}{3}+16}$=$\frac{4}{3}\sqrt{3}$����8�֣�
��3��֤�������A��B������ΪA��x1��y1����B��x2��y2�������E������Ϊ��$\frac{{x}_{1}+{x}_{2}}{2}$��$\frac{{y}_{1}+{y}_{2}}{2}$����
���������ֱ��l1�ķ���Ϊy=k��x-1����k��0����
���������߷��̣���ȥy��k2x2-��2k2+4��x+k2=0����=��2k2+4��2-4k4=16k2+16��0�� ����9�֣�
��ֱ��l1�������߽���A��B���㣬��x1+x2=2+$\frac{4}{{k}^{2}}$��y1+y1=$\frac{4}{k}$������10�֣�
���E��������1+$\frac{2}{{k}^{2}}$��$\frac{2}{k}$����
����֪��ֱ��l2��б��Ϊ-$\frac{1}{k}$��
ͬ���ɵ�F������Ϊ��1+2k2��-2k��������11�֣�
��k�١�1ʱ����1+$\frac{2}{{k}^{2}}$��1+2k2����ʱֱ��EF��б��Ϊ��kEF=$\frac{k}{1-{k}^{2}}$��
��ֱ��EF�ķ���Ϊy+2k=$\frac{k}{1-{k}^{2}}$��x-1-2k2����������y=$\frac{k}{1-{k}^{2}}$��x-3����������㣨3��0������13�֣�
��k=��1ʱ��ֱ��EF�ķ���Ϊx=3��Ҳ���㣨3��0����
����������ֱ��EF������㣨3��0��������14�֣�
���� ���⿼��켣���̵���������ֱ����������λ�ù�ϵ��Ӧ�ã������˷������۵���ѧ˼�뷽�������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
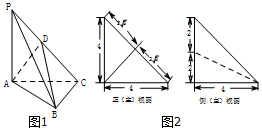 ��ͼ1��������P-ABC�У�PA��ƽ��ABC��AC��BC��DΪ����PC��һ�㣬��������������ͼ�Ͳࣨ����ͼ��ͼ2��ʾ��
��ͼ1��������P-ABC�У�PA��ƽ��ABC��AC��BC��DΪ����PC��һ�㣬��������������ͼ�Ͳࣨ����ͼ��ͼ2��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7�� | B�� | 3�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
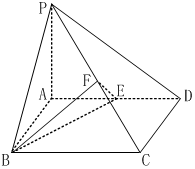 ��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��AP=AB=2��BC=2$\sqrt{2}$��E��F�ֱ���AD��PC���е㣮
��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��AP=AB=2��BC=2$\sqrt{2}$��E��F�ֱ���AD��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com