
分析 依题意,可求得f[f(x)]=(-$\sqrt{x}$+$\frac{1}{\sqrt{x}}$)6,利用二项展开式的通项公式,即可求得f[f(x)]表达式的展开式中常数项.
解答 解:当x>0时,f[f(x)]=f(-$\sqrt{x}$)=(-$\sqrt{x}$+$\frac{1}{\sqrt{x}}$)6的展开式中,
通项为Tr+1=${C}_{6}^{r}$(-$\sqrt{x}$)n-r•($\frac{1}{\sqrt{x}}$)r,
则常数项为:${C}_{6}^{3}$(-$\sqrt{x}$)3•($\frac{1}{\sqrt{x}}$)3=-20.
故答案为:-20.
点评 本题考查分段函数的运用,考查二项式系数的性质,考查运算求解能力,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形 | D. | 等腰三角形或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
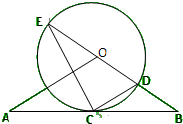 (如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
(如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1)∪(1,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 7 | C. | 3或7 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com