
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.
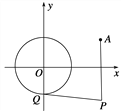
(1)求a,b间的关系;
(2)求|PQ|的最小值.
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某便利店每天以每件5元的价格购进若干鲜奶,然后以每件10元价格出售,如果当天卖不完,剩下的鲜奶作餐厨垃圾处理.便利店记录了100天这种鲜奶的日需求量![]() (单位:件)如表所示:
(单位:件)如表所示:
日需求量n(件) | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
频数 | 10 | 20 | 16 | 16 | 15 | 12 | 11 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(1)若便利店一天购进160件这种鲜奶,X表示当天的利润(单位:元),求X的分布列与数学期望及方差;
(2)若便利店一天购进160件或170件这种鲜奶,仅从获得利润大的角度考虑,你认为应购进160件还是170件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C的参数方程是![]() (θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:
(θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:![]()
(1)求曲线C的极坐标方程;
(2)设直线θ=![]() 与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径,则![]() 的取值范围是( )
的取值范围是( )
A. [![]() ,0) B. [
,0) B. [![]() ,0] C. [
,0] C. [![]() ,1) D. [
,1) D. [![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点F为圆C:
的焦点F为圆C:![]() 的圆心.
的圆心.
![]() 求抛物线的方程与其准线方程;
求抛物线的方程与其准线方程;
![]() 直线l与圆C相切,交抛物线于A,B两点;
直线l与圆C相切,交抛物线于A,B两点;
![]() 若线段AB中点的纵坐标为
若线段AB中点的纵坐标为![]() ,求直线l的方程;
,求直线l的方程;
![]() 求
求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接2000年的到来,某地组织了一次乒乓球迎春幸运赛.首先,通过身份号抽选出2000名选手,编号为1,2,…,2000,他们当中任两人都可以组成一对双打选手,每对选手的编号之和称为他们的“和号”.规定:“和号”相同的两对选手方有资格进行幸运双打赛.比赛开始前,组委会首先从2000个编号中随机抽出65名幸运选手,然后找出“和号”相同的两对选手进行幸运双打赛(凡同一“和号”的选手分在同一区进行单循环).求证:无论怎样抽选,总有选手进行幸运赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两班各派三名同学参加知识竞赛,每人回答一个问题,答对得10分,答错得0分,假设甲班三名同学答对的概率都是![]() ,乙班三名同学答对的概率分别是
,乙班三名同学答对的概率分别是![]() ,
,![]() ,
,![]() ,且这六名同学答题正确与否相互之间没有影响.
,且这六名同学答题正确与否相互之间没有影响.
(1)记“甲、乙两班总得分之和是60分”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示甲班总得分,求随机变量
表示甲班总得分,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD—A1B1C1D1中,AB=BD=1,![]() ,AA1=BC=2,AD∥BC.
,AA1=BC=2,AD∥BC.

(1)证明:BD⊥平面ABB1A1.
(2)比较四棱锥D—ABB1A1与四棱锥D—A1B1C1D1的体积的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为![]() (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程和C2的直角坐标方程;
(2)射线OP:![]() (其中
(其中![]() )与C2交于P点,射线OQ:
)与C2交于P点,射线OQ:![]() 与C2交于Q点,求
与C2交于Q点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com