解:(1)设切线的斜率为k,则k=f′(x)=2x
2-4x+3=2(x-1)
2+1,当x=1时,k
min=1.
把a=1代入到f(x)中得:f(x)=

x
3-2x
2+3x,所以f(1)=

-2+3=

,即切点坐标为(1,

)
∴所求切线的方程为y-

=x-1,即3x-3y+2=0.
(2)f′(x)=2x
2-4ax+3,因为y=f(x)为单调递增函数,则对任意的x∈(0,+∞),恒有f′(x)>0,
f′(x)=2x
2-4ax+3>0,
∴a<
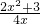
=

+
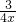
,而

+
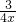
≥

,当且仅当x=

时,等号成立.
所以a<

,则所求满足条件的最大整数a值为1.
分析:(1)设出切线的斜率k,得到k等于f′(x)并把a=1代入到f(x)中求出解析式,根据二次函数求最小值的方法,求出k的最小值,然后把x=1代入到f(x)中求出f(1)的值即可得到切点坐标,根据斜率和切点坐标写出切线方程即可;
(2)求出f′(x),要使f(x)为单调递增函数,必须满足f'(x)>0,即对任意的x∈(0,+∞),恒有f′(x)大于0,解出a小于一个关系式,利用基本不等式求出这个关系式的最小值,得到关于a的不等式,求出解集即可得到a的取值范围,在范围中找出满足条件的最大整数即可.
点评:此题是一道综合题,要求学生会根据导数求出切线的斜率,掌握不等式恒成立时所取的条件,利用会利用基本不等式求函数的最小值及会求二次函数的最小值.

 x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R). x3-2x2+3x,所以f(1)=
x3-2x2+3x,所以f(1)= -2+3=
-2+3= ,即切点坐标为(1,
,即切点坐标为(1, )
) =x-1,即3x-3y+2=0.
=x-1,即3x-3y+2=0.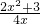 =
= +
+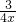 ,而
,而 +
+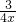 ≥
≥ ,当且仅当x=
,当且仅当x= 时,等号成立.
时,等号成立. ,则所求满足条件的最大整数a值为1.
,则所求满足条件的最大整数a值为1.

 快捷英语周周练系列答案
快捷英语周周练系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<