
分析 (Ⅰ)由函数f(x)的定义域为(0,+∞),而f′(x)=$\frac{1}{x-1}$-k.能求出函数f(x)的单调区间.
(Ⅱ)由(Ⅰ)知k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1-k>0,f(x)≤0不成立,故k>0,又由(Ⅰ)知f(x)的最大值为f($\frac{1}{k}$+1),由此能确定实数k的取值范围;
(Ⅲ)由(Ⅱ)知,当k=1时,有f(x)≤0在(0,+∞)恒成立,且f(x)在(1,+∞)上是减函数,f(1)=0,即lnx<x-1在x∈[2,+∞)上恒成立,由此能够证明(n∈N*且n>1).
解答 解:(Ⅰ)函数f(t)的定义域为(1,+∞),f′(t)=$\frac{1}{x-1}$-k.
当k≤0时,f′(t)=$\frac{1}{x-1}$-k>0,
f(x)在(1,+∞)上是增函数;
当k>0时,若x∈(0,$\frac{1}{k}$+1)时,有f′(x)>0,
若x∈($\frac{1}{k}$+1,+∞)时,有f′(x)<0,
则f(x)在(0,$\frac{1}{k}$+1)上是增函数,在($\frac{1}{k}$+1,+∞)上是减函数.
(Ⅱ)由(Ⅰ)知k≤0时,f(x)在(1,+∞)上是增函数,
而f(2)=1-k>0,f(x)≤0不成立,故k>0,
又由(Ⅰ)知f(x)的最大值为f($\frac{1}{k}$+1),要使f(x)≤0恒成立,
则f($\frac{1}{k}$+1)≤0即可,即-lnk≤0,得k≥1;
(Ⅲ)当k=1时,有f(x)≤0在(0,+∞)恒成立,
且f(x)在(2,+∞)上是减函数,f(2)=0,
即ln(x-1)<x-1-1在x∈(2,+∞)上恒成立,
令x-1=n2,则lnn2<n2-1,
即2lnn<(n-1)(n+1),
∴$\frac{lnn}{n+1}$<$\frac{n-1}{2}$(n∈N*且n>1)
∴$\frac{ln2}{3}$+$\frac{ln3}{4}$+$\frac{ln4}{5}$+…+$\frac{lnn}{n+1}$<$\frac{1}{2}$+$\frac{2}{2}$+$\frac{3}{2}$+…+$\frac{n-1}{2}$=$\frac{n(n-1)}{4}$,
即:$\frac{ln2}{3}$+$\frac{ln3}{4}$+$\frac{ln4}{5}$+…+$\frac{lnn}{n+1}$<$\frac{n(n-1)}{4}$(n∈N*且n>1)成立.
点评 本题考查函数单调区间的求法,确定实数的取值范围,不等式的证明.考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.


科目:高中数学 来源: 题型:解答题
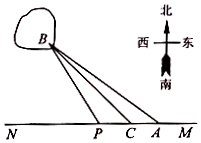 如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.
如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | (0,1] | C. | [1,+∞) | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
| 对服务好评 | 对服务不满意 | 合计 | |
| 对商品好评 | a=80 | b=40 | 120 |
| 对商品不满意 | c=70 | d=10 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3] | B. | (-1,3) | C. | [-3,1) | D. | [-3,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com