练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，将椭圆上每一点的横坐标保持不变，纵坐标变为原来的一半，得曲线C，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为．

    写出曲线C的普通方程和直线l的直角坐标方程；

    已知点且直线l与曲线C交于A、B两点，求的值．

    【答案】（1），；（2）

    【解析】

    设为椭圆上的点，在已知变换下变为C上点，依题意，得由此能求出曲线C的普通方程；由直线l的极坐标方程，能求出直线l的直角坐标方程；

    求出直线l的参数方程并代入，得：，结合，求解即可。

    将椭圆上每一点的横坐标保持不变，纵坐标变为原来的一半，得曲线C，

    设为椭圆上的点，在已知变换下变为C上点，

    依题意，得．

    由，得，

    曲线C的普通方程为．

    直线l的极坐标方程为．

    直线l的直角坐标方程为．

    点且直线l与曲线C交于A、B两点，在直线l上，

    把直线l的参数方程代入，得：，

    则，．

    ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】我市正在创建全国文明城市，某高中为了解学生的创文知晓率，按分层抽样的方法从“表演社”、“演讲社”、“围棋社”三个活动小组中随机抽取了6人进行问卷调查，各活动小组人数统计如下图：

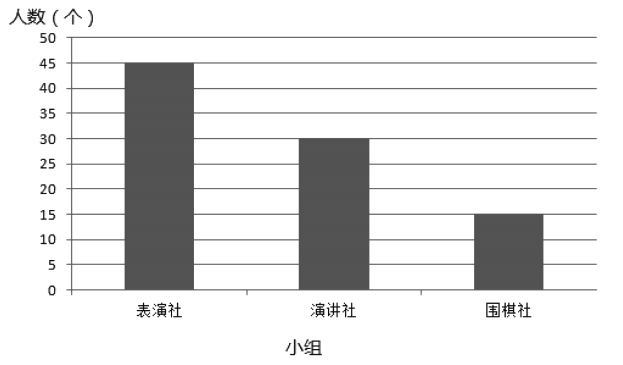
    （1）从参加问卷调查的6名学生中随机抽取2名，求这2名学生来自同一小组的概率；

    （2）从参加问卷调查的6名学生中随机抽取3名，用表示抽得“表演社”小组的学生人数，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】黄平县且兰高中全体师生努力下，有效进行了“一对一辅导战略”成绩提高了一倍，下列是“优秀学生”，“中等学生”，“差生”进行“一对一”前后所占比例

    战略前

    战略后

    优秀学生

    中等学生

    差生

    优秀学生

    中等学生

    差生

    20%

    50%

    30%

    25%

    45%

    30%

    则下列结论正确的是（ ）

    A.实行“一对一”辅导战略，差生成绩并没有提高.

    B.实行“一对一”辅导战略，中等生成绩反而下降了.

    C.实行“一对一”辅导战略，优秀学生成绩提高了.

    D.实行“一对一”辅导战略，优秀学生与中等生的成绩没有发生改变.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名学生的课外体育锻炼平均每天运动的时间(单位：分钟)进行调查，将收集的数据分成，，，，，六组，并作出频率分布直方图(如图)，将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”．

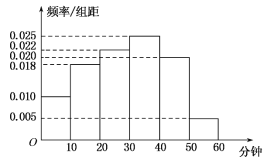
    (1)请根据直方图中的数据填写下面的2×2列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？

    课外体育不达标

    课外体育达标

    合计

    男

    60

    女

    110

    合计

    (2)现按照“课外体育达标”与“课外体育不达标”进行分层抽样，抽取8人，再从这8名学生中随机抽取3人参加体育知识问卷调查，记“课外体育不达标”的人数为X，求X的分布列和数学期望．参考公式：

    P(K2≥k0)

    0.15

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    2.072

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱柱中，，，，．

    求证：面面；

    若，在线段上是否存在一点，使二面角的平面角的余弦值为？若存在，确定点的位置；若不存在，说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆（）的离心率是，点在短轴上，且。

    （1）球椭圆的方程；

    （2）设为坐标原点，过点的动直线与椭圆交于两点。是否存在常数，使得为定值？若存在，求的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为F，直线l过点．

    （1）若点F到直线l的距离为，求直线l的斜率；

    （2）设A，B为抛物线上两点，且AB不与x轴垂直，若线段AB的垂直平分线恰过点M，求证：线段AB中点的横坐标为定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本，其选报文科理科的情况如下表所示．


    男

    女

    文科

    2

    5

    理科

    10

    3

    （Ⅰ）若在该样本中从报考文科的学生中随机地选出3人召开座谈会，试求3人中既有男生也有女生的概率；

    （Ⅱ）用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关？

    参考公式和数据：


    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001


    2.07

    2.71

    3.84

    5.02

    6.64

    7.88

    10.83

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新高考，取消文理科，实行“”，成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况，随机调查50人（把年龄在称为中青年，年龄在称为中老年），并把调查结果制成下表：

    年龄（岁）

    频数

    5

    15

    10

    10

    5

    5

    了解

    4

    12

    6

    5

    2

    1

    （1）分别估计中青年和中老年对新高考了解的概率；

    （2）请根据上表完成下面列联表，是否有95%的把握判断对新高考的了解与年龄（中青年、中老年）有关？

    了解新高考

    不了解新高考

    总计

    中青年

    中老年

    总计

    附：.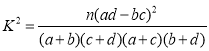

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    （3）若从年龄在的被调查者中随机选取3人进行调查，记选中的3人中了解新高考的人数为，求的分布列以及.

    查看答案和解析>>

    同步练习册答案