
【题目】已知圆的方程为(x﹣1)2+(y﹣1)2=1,P点坐标为(2,3), 求:
(1)过P点的圆的切线长.
(2)过P点的圆的切线方程.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,区间M=[a,b](a<b),集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有( )
,区间M=[a,b](a<b),集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有( )
A.1个
B.2个
C.3个
D.无数多个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: 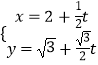 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(1)若点M的直角坐标为(2, ![]() ),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
(2)设曲线C经过伸缩变换 ![]() 得到曲线C′,求曲线C′的内接矩形周长的最大值.
得到曲线C′,求曲线C′的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
月份 | 2 | 3 | 4 | 5 |
产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图; 
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量? (注:回归方程 ![]() =
= ![]() x+
x+ ![]() 中,
中, ![]() =
= 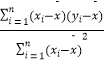 =
= 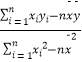 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一简单组合体,其底面ABCD为正方形,棱PD与EC均垂直于底面ABCD,PD=2EC,N为PB的中点,求证: 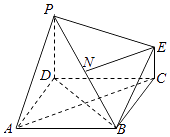
(1)平面EBC∥平面PDA;
(2)NE⊥平面PDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为2 ![]() 的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点.
的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点. 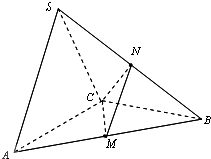
(1)证明:AC⊥SB;
(2)求三棱锥B﹣CMN的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x . (Ⅰ)试写出这个函数的性质(不少于3条,不必说明理由),并作出图象;
(Ⅱ)设函数g(x)=4x+4﹣x﹣af(x),求这个函数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明![]() ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.(3k+2)
B.(3k+4)
C.(3k+2)+(3k+3)
D.(3k+2)+(3k+3)+(3k+4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com