
【题目】下列说法中不正确的序号为____________.
①若函数![]() 在
在![]() 上单调递减,则实数
上单调递减,则实数![]() 的取值范围是
的取值范围是![]() ;
;
②函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③已知函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域是
的定义域是![]() ;
;
④若函数![]() 在
在![]() 上有最小值-4,(
上有最小值-4,(![]() ,
,![]() 为非零常数),则函数
为非零常数),则函数![]() 在
在![]() 上有最大值6.
上有最大值6.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且![]() ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.

(1)求证:EC⊥CD;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,并且图象关于y轴对称,当x≤-1时,y=f(x)的图象是经过点(-2,0)与(-1,1)的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且经过点(1,1)的一段抛物线.
(1)试求出函数f(x)的表达式,作出其图象;
(2)根据图象说出函数的单调区间,以及在每一个单调区间上函数是增函数还是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() ax2-1-lnx,其中a∈R.
ax2-1-lnx,其中a∈R.
(1)若a=0,求过点(0,-1)且与曲线y=f(x)相切的直线方程;
(2)若函数f(x)有两个零点x1,x2,
① 求a的取值范围;
② 求证:f ′(x1)+f ′(x2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
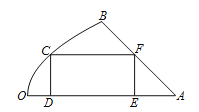
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
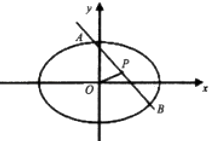
【题目】已知直线l:y=﹣x+1与椭圆C: ![]() =1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为(
=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为( ![]() ,
, ![]() )
) 
(1)求椭圆C离心率;
(2)设O为坐标原点,且2|OP|=|AB|,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如右表,则下列说法正确的是( )
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. 有99.9%的把握认为使用智能手机对学习有影响.
B. 有99.9%的把握认为使用智能手机对学习无影响.
C. 在犯错误的概率不超过0.005的前提下认为使用智能手机对学习有影响.
D. 在犯错误的概率不超过0.005的前提下认为使用智能手机对学习无影响.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两地相距![]() ,货车从甲地匀速行驶到乙地,速度不得超过
,货车从甲地匀速行驶到乙地,速度不得超过![]() ,已知货车每小时的运输成本(单位:圆)由可变本和固定组成组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:圆)由可变本和固定组成组成,可变成本是速度平方的![]() 倍,固定成本为
倍,固定成本为![]() 元.
元.
(1)将全程匀速匀速成本![]() (元)表示为速度
(元)表示为速度![]() 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2)若![]() ,为了使全程运输成本最小,货车应以多大的速度行驶?
,为了使全程运输成本最小,货车应以多大的速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宜昌市拟在2020年点军奥体中心落成后申办2022年湖北省省运会,据了解,目前武汉,襄阳,黄石等申办城市因市民担心赛事费用超支而准备相继退出,某机构为调查宜昌市市民对申办省运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为不同年龄与支持申办省运会无关?
的前提下认为不同年龄与支持申办省运会无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附: 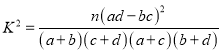 ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |