
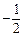 ,
,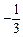 ,
,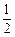 ,1,2,3}
,1,2,3} 。已知a∈A,使得幂函数
。已知a∈A,使得幂函数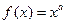 为奇函数,指数函数
为奇函数,指数函数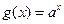 在区间(0,+∞)上为增函数。
在区间(0,+∞)上为增函数。 明理由;
明理由; (x)]。
(x)]。 ,x3=
,x3=
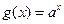 在区间(0,+∞)上为增函数,∴a>1,∴a只可能为2或3。而当a=2时,幂函数f(x)=x2为偶函数,只有当a=3时,幂函数f(x)=x3为奇函数
在区间(0,+∞)上为增函数,∴a>1,∴a只可能为2或3。而当a=2时,幂函数f(x)=x2为偶函数,只有当a=3时,幂函数f(x)=x3为奇函数 故a=3…3分
故a=3…3分 =
= ,
, x2,∴x1-x2<0,
x2,∴x1-x2<0, >0,∴f(x1)-f(x2)>0,∴f(x1)>f(x2)。
>0,∴f(x1)-f(x2)>0,∴f(x1)>f(x2)。 ....10分
....10分 ,x3=
,x3= 。 …12分
。 …12分

 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:不详 题型:单选题
 ,当
,当 取不同的正数时,在区间
取不同的正数时,在区间 上它们的图像是一族美丽的曲线(如图).设点
上它们的图像是一族美丽的曲线(如图).设点 ,连接AB,线段AB恰好被其中的两个幂函数
,连接AB,线段AB恰好被其中的两个幂函数 的图像三等分,即有
的图像三等分,即有 那么,ab=( )
那么,ab=( )A. | B. | C.2 | D.1 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 在定义域上递增。
在定义域上递增。 的解析式;
的解析式; ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com