
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.
【答案】(Ⅰ) ![]() =6.6x138.6.(Ⅱ)(i)答案见解析;(2)190.
=6.6x138.6.(Ⅱ)(i)答案见解析;(2)190.
【解析】试题分析:
(Ⅰ)根据所给公式及数据求得![]() ,从而可得线性回归方程.(Ⅱ) ( i )根据所给数据求出相关指数为R2
,从而可得线性回归方程.(Ⅱ) ( i )根据所给数据求出相关指数为R2![]() ,通过比较可得回归方程为
,通过比较可得回归方程为![]() =0.06e0.2303x的拟合效果好.( ii )当x=35时,求出
=0.06e0.2303x的拟合效果好.( ii )当x=35时,求出![]() =0.06e0.2303x的值即为预测值.
=0.06e0.2303x的值即为预测值.
试题解析:
(Ⅰ)由题意得, 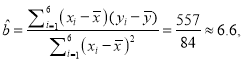
∴![]() 336.626=138.6,
336.626=138.6,
∴y关于x的线性回归方程为![]() =6.6x138.6.
=6.6x138.6.
(Ⅱ) ( i )由所给数据求得的线性回归方程为![]() =6.6x138.6,相关指数为
=6.6x138.6,相关指数为
R2=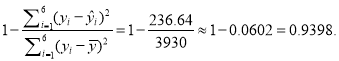
因为0.9398<0.9522,
所以回归方程![]() =0.06e0.2303x比线性回归方程
=0.06e0.2303x比线性回归方程![]() =6.6x138.6拟合效果更好.
=6.6x138.6拟合效果更好.
( ii )由( i )得当温度x=35C时, ![]() =0.06e0.230335=0.06e8.0605.
=0.06e0.230335=0.06e8.0605.
又∵e8.0605≈3167,
∴![]() ≈0.063167≈190(个).
≈0.063167≈190(个).
即当温度x=35C时,该种药用昆虫的产卵数估计为190个.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,

(1)画出函数f(x),x∈R剩余部分的图象,并根据图象写出函数f(x),x∈R的单调区间;(只写答案)
(2)求函数f(x),x∈R的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒中装有编号分别为![]() 的四个形状大小完全相同的小球.
的四个形状大小完全相同的小球.
(1)从盒中任取两球,求取出的球的编号之和大于![]() 的概率.
的概率.
(2)从盒中任取一球,记下该球的编号![]() ,将球放回,再从盒中任取一球,记下该球的编号
,将球放回,再从盒中任取一球,记下该球的编号![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为0?若存在,求出
的最小值为0?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数,使得
,若存在实数,使得![]() 成立,则x0称为f(x)的“不动点”.
成立,则x0称为f(x)的“不动点”.
(1)设函数![]() ,求
,求![]() 的不动点;
的不动点;
(2)设函数![]() ,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
(3)设函数![]() 定义在
定义在![]() 上,证明:若
上,证明:若![]() 存在唯一的不动点,则
存在唯一的不动点,则![]() 也存在唯一的不动点.
也存在唯一的不动点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: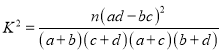 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com